Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

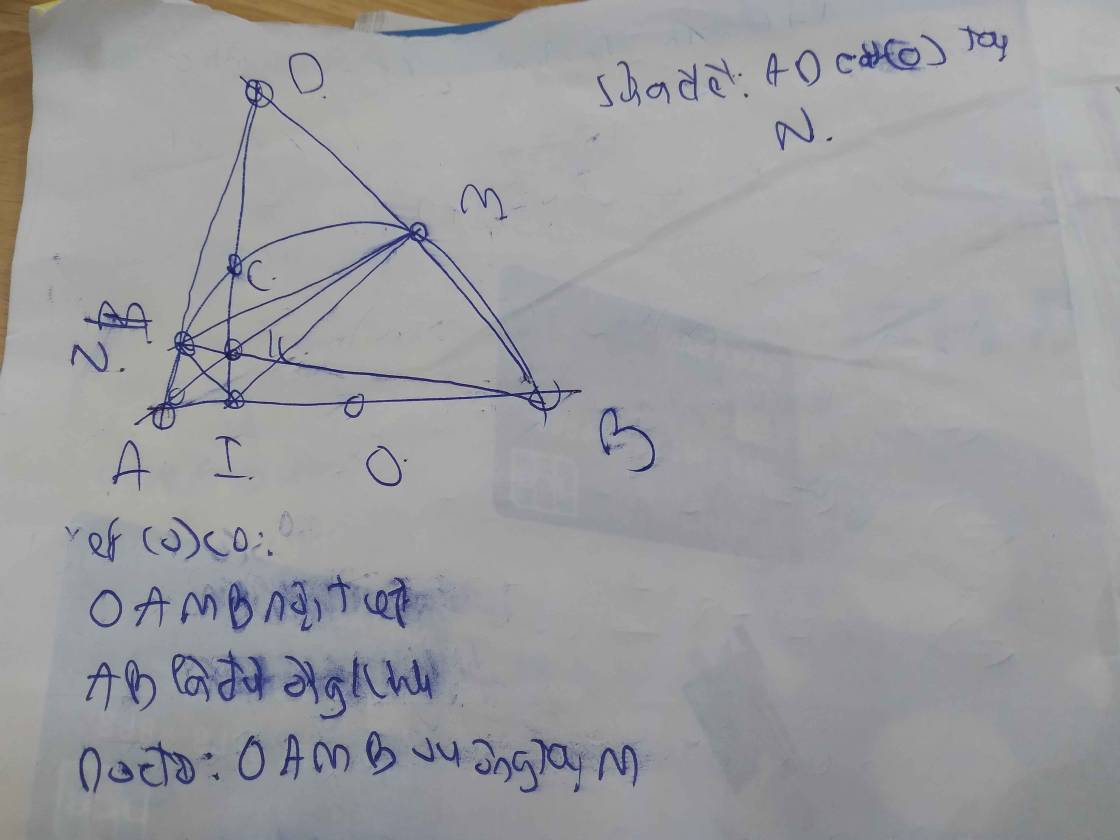
a: Xét (O) có
ΔBEA nội tiếp
BA là đường kính
=>ΔBEA vuông tại E
góc MCA+góc MEA=90+90=180 độ
=>MCAE nội tiếp
b: góc BFA=1/2*sđ cung BA=1/2*180=90 độ
Xét ΔBFA vuông tại F và ΔBCN vuông tai C có
góc B chung
=>ΔBFA đồng dạng với ΔBCN
=>BF/BC=BA/BN
=>BC*BA=BF*BN
Xét ΔBEA vuông tại E và ΔBCM vuông tại C có
góc EBA chung
=>ΔBEA đồng dạng với ΔBCM
=>BE/BC=BA/BM
=>BC*BA=BE*BM=BF*BN

a: MB là tiếp tuyến của (O), B là tiếp điểm
nên MB\(\perp\)BO tại B
=>ΔBOM vuông tại B
b:
ΔOBH vuông tại H
=>\(BH^2+HO^2=BO^2\)
=>\(BH^2=5^2-3^2=16\)
=>BH=4(cm)
Xét ΔOBM vuông tại B có BH là đường cao
nên \(OH\cdot OM=OB^2\)
=>\(OM=\dfrac{5^2}{3}=\dfrac{25}{3}\left(cm\right)\)
ΔOBM vuông tại B
=>\(OB^2+BM^2=OM^2\)
=>\(BM^2+5^2=\left(\dfrac{25}{3}\right)^2\)
=>\(BM^2=\dfrac{625}{9}-25=\dfrac{400}{9}\)
=>BM=20/3(cm)
c: ΔOBC cân tại O
mà OH là đường cao
nên OH là phân giác của \(\widehat{BOC}\)
Xét ΔOBM và ΔOCM có
OB=OC
\(\widehat{BOM}=\widehat{COM}\)
OM chung
Do đó: ΔOBM=ΔOCM
=>\(\widehat{OBM}=\widehat{OCM}=90^0\)
=>MC là tiếp tuyến của (O)
d: Xét tứ giác OBMC có
\(\widehat{OBM}+\widehat{OCM}=90^0+90^0=180^0\)
=>OBMC là tứ giác nội tiếp đường tròn đường kính OM
Tâm là trung điểm của OM

Gọi A' là giao điểm của đường tròn ngoại tiếp tam giác AEF và tia AB
Ta chứng minh được E,A,N và M, A, F thẳng hàng
=> A đối xứng với A' qua C => B đối xứng với A' qua điểm A mà A' cố định
=> Tâm I của đường tròn ngoại tiếp tam giác BMN nằm trên đường trung trực của đoạn thẳng BA'.