Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

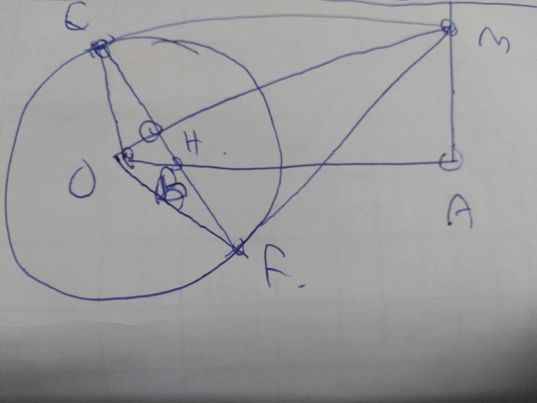
O A M E F H B I
Hướng dẫn giải:
a) Do ME, MF là tiếp tuyến với đường tròn suy ra EF ⊥ OM
Tứ giác ABHM có góc A = góc H = 900 nên tứ giác này nội tiếp đường tròn bán kính MB.
b) \(Δ_VOHB ∼ Δ_VOAM\) (g.g)
\(\Rightarrow \dfrac{OH}{OA}=\dfrac{OB}{AM}\)
\(\Rightarrow OA.OB=OH.OM\) (1)
\(Δ_VOHE∼ Δ_VOEM\) (g.g)
\(\Rightarrow \dfrac{OH}{OE}=\dfrac{OE}{OM}\)
\(\Rightarrow OH.OM=OE^2=R^2\)(2)
Từ (1) và (2) suy ra \(OA.OB=OH.OM =R^2\)
c) Gọi I là giao điểm của OM với đường tròn (O). Nối FI.
Do \(\stackrel\frown{FI}=\stackrel\frown{EI}\) suy ra \(\widehat{MFI}=\widehat{EFI}\)
Suy ra FI là phân giác của góc \(\widehat{MFE}\)
Lại có MI là phân giác của góc \(\widehat{EMF}\)
Do đó I là giao điểm của đường phân giác trong của tam giác MEF
\(\Rightarrow\) I là tâm đường tròn nội tiếp tam giác MEF.
Mà I thuộc đường tròn (O) cố định. Suy ra đpcm.
d) Diện tích tam giác HBO: \(S=\dfrac{1}{2}HO.HB\)
Xét \(Δ_VOHB∼ Δ_VOAM\) (g.g)
\(\Rightarrow \dfrac{HB}{AM}=\dfrac{OB}{OM}\)
\(\Rightarrow HB.OM=AM.OB\) (3)
Có: \(OH.OM=R^2\) (4)
Nhân (3) và (4) vế với vế ta được: \(OH.HB.OM^2=R^2.AM.OB=R^2.AM.\dfrac{R^2}{OA}\)
\(\Rightarrow OH.HB = R^4.\dfrac{AM}{OA.OM^2}= R^4.\dfrac{AM}{OA.(OA^2+AM^2)}\)
Áp dụng BĐT Cô si với OA và AM ta có: \(OA^2+AM^2\ge2.\sqrt{OA^2.AM^2}=2.OA.AM\)
Dấu "=" xảy ra khi: \(OA=AM\)
\(\Rightarrow OH.HB \le R^4.\dfrac{AM}{OA.2.OA.AM}=\dfrac{R^4}{2OA^2}\)
Suy ra: \(S_{max}=\dfrac{R^4}{4.OA^2}\) khi \(OA=AM\)

a:Xét (O) có
MF,ME là tiếp tuyến
Do đó: MF=ME
=>M nằm trên đường trung trực của FE(1)
OE=OF
=>O nằm trên đường trung trực của EF(2)
Từ (1) và (2) suy ra OM là đường trung trực của EF
=>OM\(\perp\)EF tại H và H là trung điểm của EF
b: ΔOMF vuông tại F
=>\(FO^2+FM^2=OM^2\)
=>\(FM^2=10^2-6^2=64\)
=>\(FM=\sqrt{64}=8\left(cm\right)\)
Xét ΔOFM vuông tại F có FH là đường cao
nên \(OH\cdot OM=OF^2\)
\(\Leftrightarrow OH\cdot10=6^2=36\)
=>OH=36/10=3,6(cm)
c: Xét tứ giác BHMA có
\(\widehat{BHM}+\widehat{BAM}=90^0+90^0=180^0\)
=>BHMA là tứ giác nội tiếp
=>B,H,M,A cùng thuộc một đường tròn

Bài 4:
a:
Xét (O) có
ΔCED nội tiếp
CD là đường kính
=>ΔCED vuông tại E
ΔOEF cân tại O
mà OI là đường cao
nên I là trung điểm của EF
Xét tứ giác CEMF có
I là trung điểm chung của CM và EF
CM vuông góc EF
=>CEMF là hình thoi
=>CE//MF
=<MF vuông góc ED(1)
Xét (O') có
ΔMPD nội tiêp
MD là đường kính
=>ΔMPD vuông tại P
=>MP vuông góc ED(2)
Từ (1), (2) suy ra F,M,P thẳng hàng
b: góc IPO'=góc IPM+góc O'PM
=góc IEM+góc O'MP
=góc IEM+góc FMI=90 độ
=>IP là tiếp tuyến của (O')