Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

a) Tứ giác ACEH có
ˆACE=ˆEHA=900ACE^=EHA^=900(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> ˆEAH=ˆHCEEAH^=HCE^(cùng chắn EH)
lại có ˆADF=ˆACFADF^=ACF^(cùng chắn AF)
mà ˆACF+ˆHCE=900ACF^+HCE^=900do ˆACE=900ACE^=900
=>ˆEAH+ˆADF=900EAH^+ADF^=900
=> DF⊥ABDF⊥AB
mà EH⊥ABEH⊥AB
=> DF//EHDF//EH
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D

a) Tứ giác ACEH có
\(\widehat{ACE}=\widehat{EHA}=90^0\)(cùng nhìn AE)
=> tứ giác ACHE nội tiếp
b) tứ giác ACHE nội tiếp
=> \(\widehat{EAH}=\widehat{HCE}\)(cùng chắn EH)
lại có \(\widehat{ADF}=\widehat{ACF}\)(cùng chắn AF)
mà \(\widehat{ACF}+\widehat{HCE}=90^0\)do \(\widehat{ACE}=90^0\)
=>\(\widehat{EAH}+\widehat{ADF}=90^0\)
=> \(DF\perp AB\)
mà \(EH\perp AB\)
=> \(DF//EH\)
c)các bước chứng minh nè :
cm HOD=DCH (2 góc cùng nhìn DH)
thì => COHD nọi tiếp đường tròn thì đường tròn sẽ đi qau C H O D

a) xét tứ giác CDFE có
EF // CD (cùng vuông góc AB)
=> góc DEF= góc EDC (1)
gọi M là giao điểm AB và CD. AB vuông góc CD => M là trung điềm CD
.........=> góc ACD = góc ADC (2)
(1),(2) => góc DEF= góc EDC => CDFE nội tiếp
b) ta có CDFE nội tiếp (cmt) => góc ECF = góc EDF =90 độ (3)
góc ADB =90 độ (góc nội tiếp chắn nửa đường tròn)(4)
(3),(4) => góc EDF + góc ADB =180 độ
=> B,D,F thẳng hàng.
c) ta có tứ giác EHAC có góc H + góc C=180 độ
=> EHAC nội tiếp
=> góc HCA = góc HEA
mà góc HEA=góc ADC(cmt)
mà góc ADC=góc ABC (=1/2sđ cung AC)
=>góc HCA=ABC
=> HC là tiếp tuyến của đường tròn tâm (O)

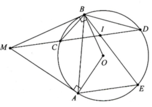
a, Vì M B C ^ = M D B ^ = 1 2 s đ C B ⏜ nên chứng minh được ∆MBC:∆MDB (g.g)
b, Vì
M
B
O
^
+
M
A
O
^
=
180
0
nên tứ giác MAOB nội tiếp
c, Đường tròn đường kính OM là đường tròn ngoại tiếp tứ giác MAOB => r = M O 2
Gọi H là giao điểm của AB với OM
=> OH ⊥ AB; AH = BH = R 3 2
Giải tam giác vuông OAM, đường cao AH ta được OM = 2R Þ r = R
d, Ta có M I B ^ = s đ D E ⏜ + s đ B C ⏜ 2 và M A B ^ = s đ A C ⏜ + s đ B C ⏜ 2
Vì AE song song CD => s đ D E ⏜ = s đ A C ⏜ => M I B ^ = M A B ^
Do tứ giác MAIB nội tiếp hay 5 điểm A, B, O, I, M nằm trên cùng 1 đường tròn kính MO
Từ đó ta có được M I O ^ = 90 0 => OI ⊥ CD hay I là trung điểm của CD


