Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:
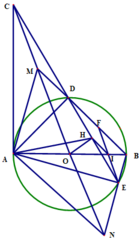
Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
=>AM vuông góc BC tại M
ΔCAB vuông tại A có AM là đường cao
nên CA^2=CM*CB
2:
D,M,B,E cùng thuộc (O)
=>DMBE nội tiếp
=>góc MDE+góc MBE=180 độ
=>góc CDM=góc CBE
Xét ΔCDM và ΔCBE có
góc CDM=góc CBE
góc DCM chung
Do đó: ΔCDM đồng dạng với ΔCBE
=>CD/CB=CM/CE
=>CD*CE=CM*CB
3: ΔOAK cân tại O
mà OH là đường cao
nên OH là phân giác của góc AOK
Xét ΔCAO và ΔCKO có
OA=OK
góc COA=góc KOC
OC chung
Do đó: ΔCAO=ΔCKO
=>góc CKO=90 độ
=>CK là tiếp tuyến của (O)

bạn tham khảo ở đây nha,mình từng giải rồi
https://hoc24.vn/cau-hoi/cho-duong-tron-o-duong-kinh-ab-tren-tiep-tuyen-tai-a-cua-duong-trong-o-lay-diem-c-ve-tuyep-tuyen-cn-va-cat-tuyen-cde-tia-cd-nam-giua-2-tai-ca-co-de-thuoc-duong-tron-o-d-nam-giua-c-va-e.1081799079177

a) Vì CA là tiếp tuyến \(\Rightarrow\angle CAD=\angle CEA\) (góc tạo bởi tiếp tuyến và dây cung bằng góc nội tiếp chắn cung đó)
Xét \(\Delta CAD\) và \(\Delta CEA:\) Ta có: \(\left\{{}\begin{matrix}\angle CAD=\angle CEA\\\angle ACEchung\end{matrix}\right.\)
\(\Rightarrow\Delta CAD\sim\Delta CEA\left(g-g\right)\Rightarrow\dfrac{CA}{CE}=\dfrac{CD}{CA}\Rightarrow CA^2=CD.CE\)
mà \(CH.CO=CA^2\) (hệ thức lượng) \(\Rightarrow CD.CE=CH.CO\)
c) Vì AB là đường kính \(\Rightarrow\angle ADB=90\)
Vì CA,CN là tiếp tuyến \(\Rightarrow\Delta CAN\) cân tại C có CO là phân giác \(\angle ACN\)
\(\Rightarrow CO\bot AN\Rightarrow\angle AHM=90\)
\(\Rightarrow\angle AHM=\angle ADM=90\Rightarrow ADHM\) nội tiếp
Ta có: \(\angle EAF=\angle DAE-\angle DAF=180-\angle DBE-\angle CHD\) (ADHM,ADBE nội tiếp)
Ta có: \(CD.CE=CH.CO\Rightarrow\dfrac{CD}{CO}=\dfrac{CH}{CE}\)
Xét \(\Delta CHD\) và \(\Delta CEO:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{CD}{CO}=\dfrac{CH}{CE}\\\angle OCEchung\end{matrix}\right.\)
\(\Rightarrow\Delta CHD\sim\Delta CEO\left(c-g-c\right)\Rightarrow\angle CHD=\angle CEO\Rightarrow DHOE\) nội tiếp
\(\Rightarrow\angle CHD=\angle CEO=\angle DEO=\dfrac{180-\angle DOE}{2}=90-\dfrac{1}{2}\angle DOE\)
\(=90-\angle DBE\Rightarrow\angle EAF=180-\angle DBE-\left(90-\angle DBE\right)=90\)
\(\Rightarrow EF\) là đường kính \(\Rightarrow E,O,F\) thẳng hàng


a) Ta có
C A B ⏜ = 90 0 O H C ⏜ = 90 0 ⇒ C A B ⏜ + O H C ⏜ = 180 0
Vậy tứ giác AOHC nội tiếp.
b) Ta có C A D ⏜ = A E C ⏜ , A C E ⏜ chung suy ra Δ A C D ~ Δ E C A (g.g)
⇒ C A C E = A D A E ⇒ A C . A E = A D . C E
c) Từ E vẽ đường thẳng song song với MN cắt cạnh AB tại I và cắt cạnh BD tại F ⇒ H E I ⏜ = H C O ⏜ .
Vì tứ giác AOHC nội tiếp ⇒ H A O ⏜ = H C O ⏜ = H E I ⏜ .
Suy ra tứ giác AHIE nội tiếp ⇒ I H E ⏜ = I A E ⏜ = B D E ⏜ ⇒ H I / / B D .
Mà H là trung điểm của DE=> I là trung điểm của EF. Có EF//MN và IE= IF
=> O là trung điểm của đoạn thẳng MN.
Suy ra tứ giác AMBN là hình bình hành => AM//BN.