Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

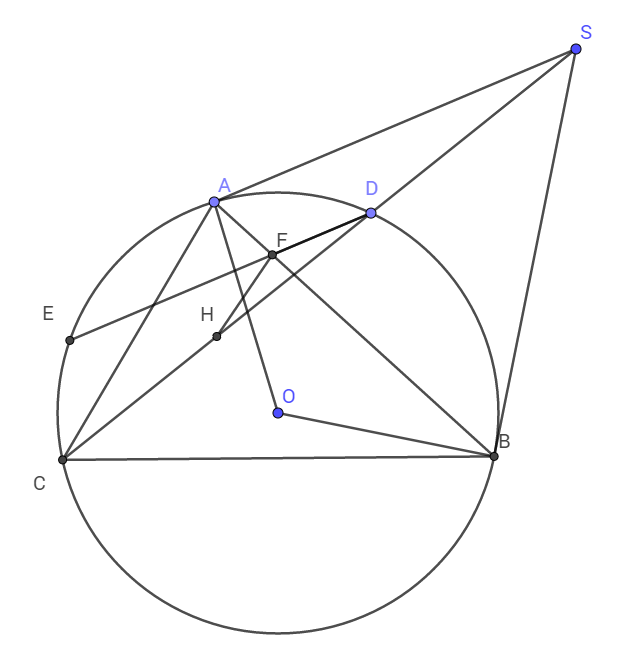
Ta có các tam giác vuông AOS; HOS, BOS có chung cạnh huyền OS nên S, A, H, O, B nội tiếp đường tròn đường kính OS.
Khi đó ta có :
\(\widehat{ASH}=\widehat{ABH}\) (Hai góc nội tiếp cùng chắn cung AH)
Mà \(\widehat{ASH}=\widehat{FDH}\) (Hai góc đồng vị)
\(\Rightarrow\widehat{ABH}=\widehat{FDH}\)
Suy ra tứ giác HFDO nội tiếp.
Từ đó ta có \(\widehat{FHD}=\widehat{ABD}\)(Hai góc nội tiếp)
Mà \(\widehat{ABD}=\widehat{ACD}\) (Hai góc nội tiếp)
Nên \(\widehat{FHD}=\widehat{ACD}\)
Chúng lại ở vị trí đồng vị nên HF // AC.

Nối BE, CE .
Vì AB=AC=> góc AEB= góc AEC. (1)
Vì tứ giác ABEC nội tiếp => góc ABC= góc AEC (2)
Kết hợp (1) và (2) => Góc AEB= góc ABC
Xét tam giác ABD và tam giác AEB có: góc ABC= góc AEB
góc BAE chung
=> 2 tam giác đồng dạng.
=> AB/AE= AD/AB => AB^2=AD.AE
nối BE và CE lại
Ta có: AB // AC \(\Rightarrow\widehat{ABC}=\widehat{AEC}\)
Tứ giác ABEC là tứ giác nội tiếp ( gt )
\(\Rightarrow\widehat{ABC}=\widehat{AEC}\)
Vì \(\widehat{ABC}=\widehat{AEC};\widehat{AEB}=\widehat{ABC}\left(cmt\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{AEB}\)
Ta có 2 tam giác ABD và AEB đồng dạng vì: \(\widehat{ABC}=\widehat{AEB};\widehat{BAE}\)chung
\(\Rightarrow\frac{AB}{AE}=\frac{AD}{AB}\Rightarrow AB^2=AD.AE\left(đpcm\right)\)
P/s đây là toán lớp 8 mà ???????

a: Xét tứ giác OBAC có
góc OBA+góc OCA=180 độ
nên OBAC là tứ giác nội tiêp
Tâm là trung điểm của OA
b: Xét tứ giác OHAC có
góc OHA+góc OCA=180 độ
=>OHAC là tứ giác nội tiếp
=>góc CHA=góc AOC
Xét tứ giác OHBA có
góc OHA=góc OBA=90 độ
nên OHBA là tứ giác nội tiếp
=>góc BHA=góc BOA=góc COA=góc CHA
=>HA là phân giác của góc BHC

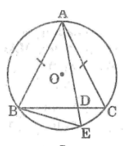

Do \(AB=AC\Rightarrow\widehat{ABC}=\widehat{AEB}\) (hai góc nt chắn 2 cung bằng nhau)
Xét 2 tam giác ADB và ABE có:
\(\left\{{}\begin{matrix}\widehat{BAD}\text{ chung}\\\widehat{ABD}=\widehat{AEB}\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ADB\sim\Delta ABE\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AB}{AE}\Rightarrow AB^2=AD.AE\)