Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

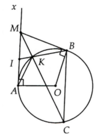
a, ∆IAK:∆IBA => I A I B = I K I A
Mà IA = IM => I M I B = I K I M
=> ∆IKM:∆IMB
b, Chứng minh được: I M K ^ = K C B ^ => BC//MA(đpcm)

Mình chỉ nói gợi ý thôi, bạn tự phát triển nhé:
Câu a)
- CM: \(MO\)song song với \(NB\).
- CM: tam giác \(MAO\) và \(NOB\) bằng nhau.
- CM: \(OMNB\) là hình bình hành.
Câu b)
- CM: \(MAON\)là hình chữ nhật.
- CM: \(H\) là giao của \(MO\) và \(AN\)
- Gọi \(D\) là hình chiếu của \(H\) lên \(AB\). CM: \(D\) là trung điểm \(AO\).
- CM: \(H\) di động trên đường cố định.

Mình không vẽ được hình mong bạn thông cảm
a, Chắc bạn làm rồi
b, Sử dụng tính chất 2 tiếp tuyến cắt nhau
=>\(\hept{\begin{cases}AP=IP\\IQ=BQ\\MA=MB\end{cases}}\)
Khi đó \(P_{MPQ}=MP+AP+MQ+QB=MA+MB=2a\)(đpcm)
c, Vì H là trực tâm của tam giác MAB
=>\(AH\perp MB\)
MÀ \(MB\perp OB\)
=> \(AH//OB\)
CMTT=>\(BH//AO\)
=> tứ giác AHBO là hình bình hành
=>AH=OB=R
MÀ A cố định
=> \(H\in\left(A,R\right)\)cố định
Vậy H thuộc đường tròn tâm A bán kính R cố định