Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
Do đó: ΔAMB vuông tại M
Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó: ΔACB vuông tại C
Xet ΔNAB có
AC.BM là các đường cao
AC cắt BM tại E
Do đó: E là trực tâm
=>NE vuông góc với AB
b: Xét tứ giác NEAF có
M là trung điểm chung của NA và EF
nên NEAF là hình bình hành
=>NE//AF
=>AF vuông góc với AB
=>FA là tiêp tuyến của (O)

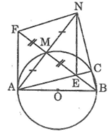
Ta có: MA = MN (tính chất đối xứng tâm)
ME = MF (tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi đường nên nó là hình bình hành
Suy ra: AF // NE
Mà NE ⊥ AB (chứng minh trên)
Suy ra: AF ⊥ AB tại A
Vậy FA là tiếp tuyến của đường tròn (O).

Bạn tự vẽ hình nha ;)
a) Xét đg tròn (O), đg kính AB có:
\(\left\{\begin{matrix}C\in\left(O\right)\\M\in\left(O\right)\end{matrix}\right.\Rightarrow\left\{\begin{matrix}\Delta ABC\\\Delta ABM\end{matrix}\right.vuông \Rightarrow\left\{\begin{matrix}AC\perp BN\\BM\perp AN\end{matrix}\right.\)
Xét \(\Delta ABN\) có: \(\left\{\begin{matrix}AC\perp BN\\BM\perp AN\end{matrix}\right.\)(c/m trên)
Mà AC và BN cắt nhau tại E
=> \(NE\perp AB\)
b) Gọi giao điểm của NE và AB là I => \(NI\perp AB\)
Xét tứ giác AENF có: AN cắt EF tại M
Mà M là trung điểm của AN( A đx với N qua M)
M là trung điểm của EF(E đx với F qua M)
=> AENF là hình bình hành( Tứ giác có 2 đ/c cắt nhau tại trung điểm của mỗi đg là hình bình hành) => AF // EN => \(\widehat{NAF}=\widehat{ANI}\) (1) ( 2 góc so le trong)
Xét \(\Delta ANI\) vuông tại I( NI\(\perp AB\)) có: \(\widehat{ANI}+\widehat{NAI}=90^o\) (2) ( 2 góc nhọn phụ nhau)
Từ (1) và (2) => \(\widehat{NAF}+\widehat{NAI}=90^o\) => \(\widehat{OAF}=90^o\) => OA\(\perp\)FAtại A
Xét đg tròn(O; OA) có: \(OA\perp FA\) tại A(c/m trên)
=> FA là tiếp tuyến của đg tròn (O)
c) Xét \(\Delta ABN\) có:
BM là trung tuyến ứng vs AN( M là trung điểm của AN)
đồng thời BM là đg cao ứng vs AN
=> \(\Delta ABN\) cân tại B( Nếu một tam giác có đg trung tuyến ứng vs một cạnh, đồng thời là đg cao ứng vs cạnh đó thì tam giác đó là tam giác cân)
=> BA=BN và BM là phân giác của góc B
=> BN là bán kính của (B)
Xét \(\Delta ABFvà\Delta NBFcó:\)
BA=BN( c/m trên)
\(\widehat{ABF}=\widehat{NBF}\)(BM là phân giác của \(\widehat{B}\))
BF là cạnh chung
=> \(\Delta ABF=\Delta NBF\left(c.g.c\right)\)
=> \(\widehat{A}=\widehat{N}\)( 2 góc tương ứng). Mà \(\widehat{A}=90^o\)
=> \(\widehat{N}=90^o\) => \(BN\perp NF\) tại N
Xét đg tròn (B;BN) có: BN\(\perp\)NF tại N( c/m trên)
=> NF là tiếp tuyến của đg tròn (B;BA)
d) Xét \(\Delta NBF\) vuông tại N(\(\widehat{N}=90^o\)) có:
\(NB^2=BM.BF\) (3)(Hệ thức lượng trong tam giác vuông)
Mặt khác \(NB^2+NF^2=BF^2\)(Định lý Pytago)
=> \(NB^2=BF^2-NF^2\) (4)
Từ (3) và (4) => \(BM.BF=BF^2-NF^2\)(cùng =\(NB^2\))

A F N M O C B E
a) Xét tam giác AMB có :
MO = OA = OB ( =bk )
\(\Rightarrow MO=\frac{1}{2}AB\)
=> Tam giác AHB vuông tại M
=> EM là đường cao của tam giác ANE
- Xét tam giác ACB có : OC = OB = OA ( =bk )
\(\Rightarrow OC=\frac{1}{2}AB\Rightarrow\Delta ACB\)vuông tại C
=> NC là đường cao của tam giác ANE
=> B là giao điểm 3 đường cao của tam giác ANE
=> AB là đường cao của tam giác ANE
Vậy : \(NE\perp AB\left(đpcm\right)\)
b) Xét 2tam giác : MAF và MNE
Có : MA = MN (gt)
MF = ME ( gt )
^AMF = ^NME ( đối đỉnh )
do đó : \(\Delta MAF=\Delta NME\left(c-g-c\right)\)
=> ^AFM = ^NEM
Mà 2 góc ^AFM và ^NEM có vị trí so le
=> AF // NE
Mà : \(NE\perp AB\)( c/m câu a ) => \(AF\perp AB\)tại A
Vậy : FA là tiếp tuyến đường tròn (O) ( đpcm )
c) Ta có : ^AMB = 90^o => \(FB\perp AN\)
MA = MB
=> FB là đường trung trực của AN
=> BN = BA ; FN = FA
- Xét 2 tam giác : ABF và NBF có : BN = BA ; FN = FA
FB chung
\(\Rightarrow\Delta ABF=\Delta NBF\left(c-c-c\right)\)
=> ^BNF = ^BAF = 90^o
\(\Rightarrow BN\perp FN\)tại B mà BN = BA
Vậy : FN là tiếp tuyến của đường tròn ( B ; BA ) ( đpcm )

A O B F N M E C
a. Xét tam giác NAB có đường cao AC,BM
mà AC,BM cắt nhau tại E
=> E là trực tâm tam giác NAB
=>NE là đường cao
\(\Rightarrow NE\perp AB\) (đpcm)
b. Vì N là điểm đối xứng với A qua M
=> M là trung điểm của AN
Vì F là điểm đối xứng với E qua M
=> M là trung điểm của EF
=> Tứ giác AFNE là hình bình hành
=> NE//AF
mà \(NE\perp AB\)
\(\Rightarrow AF\perp AB\)
=> AF là tiếp tuyến của (O) (đpcm)
c. Vì tam giác BAN có đường cao BM, đường trung tuyến BM
\(\Rightarrow\Delta BAN\)cân tại B
=> BM là đường phân giác
Xét ΔBAF và ΔBNF có:
BA = BN
BF chung
góc ABF= góc NBF ( vì BF là đường phân giác)
Suy ra : ΔBAF = ΔBNF (c.g.c)
-> góc BAF=góc BNF =900
\(\Rightarrow BN\perp NF\)
=> FN là tiếp tuyến của đường tròn (B,BN) hay đường tròn (B,BA) (đpcm)
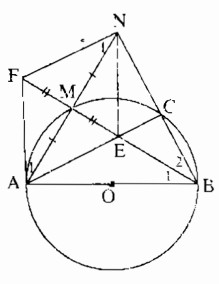
a) Tam giác ABM nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại M
Suy ra: AN ⊥ BM
Tam giác ABC nội tiếp trong đường tròn (O) có AB là đường kính nên vuông tại C
Suy ra: AC ⊥ BN
Tam giác ABN có hai đường cao AC và BM cắt nhau tại E nên E là trọng tâm của tam giác ABN
Suy ra: NE ⊥ AB
b) Ta có: MA = MN ( tính chất đối xứng tâm)
ME = MF ( tính chất đối xứng tâm)
Tứ giác AENF có hai đường chéo cắt nhau tại trung điểm của mỗi điểm đường nên nó là hình bình hành.
Suy ra: AF // NE
Mà NE ⊥ AB ( chứng minh trên)
Suy ra: AF ⊥ AB tại A.
Vậy FA là đường trung tuyến của đường tròn (O).
c) Trong tam giác ABN ta có: AN ⊥ BM và AM = AN
Suy ra tam giác ABN cân tại B.
Suy ra BA = BN hay N thuộc đường tròn (B; BA)
Tứ giác AFNE là hình bình hành nên AE // FN hay FN // AC
Mặt khác: AC ⊥ BN ( chứng minh trên)
Suy ra: FN ⊥ BN tại N
Vậy FN là tiếp tuyến của đường tròn ( B; BA).

Em vừa giải ra, nhưng hy vọng tìm được cách đơn giản hơn.
Cách của em:
a+ b)
Dễ có AN là đường trung trực FE nên AF = FE.
^FAE=180o - 2. ^AEF = 180o - 2. ^CEB = 2. ^EBC
Dễ có BM là đường trung trực AN nên BN = BA.
Do đó tam giác NBA cân tại B.
Vậy BM là đường trung trực đồng thời là phân giác.
Vậy ^EBC = ^ABE suy ra ^FAE = 2. ^EBC = ^EBC +^ABE = ^CBA.
Ta có: ^FAB = ^FAE+^CAB=^CBA +^CAB = 90o
Vậy FA là tiếp tuyến (O) (1)
Mặt khác tứ giác FNEA có FM = ME; MN = MA nên là hình bình hành.
Vậy FA // NE (2)
Từ (1) và (2) suy ra NE vuông góc với AB.
c) BM là đường trung trực AN nên BF là đường trung trực AN
Có ngay FN = FA \(\Rightarrow\widehat{FNA}=\widehat{FAN}\)
Dễ chứng minh $\Delta MBN = \Delta MBA$ nên $\widehat{ANB}=\widehat{NAB}$
$\widehat{FNB}=\widehat{FAN}+\widehat{NAB}=\widehat{FAB}=90^o$
d) $BF^2-FN^2 =BN^2 = BM \cdot BF$
Em nghĩ quá phức tạp :D
\(\widehat{AMB}\) và \(\widehat{ACB}\) đều là góc nội tiếp chắn nửa đường tròn nên AC và BM là 2 đường cao của tam giác ABN
\(\Rightarrow\) E là trực tâm \(\Rightarrow NE\) là đường cao thứ 3 \(\Rightarrow NE\perp AB\)
