K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

19 tháng 4 2023
1: Tọa độ A là:
y=0 và 4x+m-3=0
=>x=(-m+3)/4 và y=0
=>OA=|m-3|/4
Tọa độ B là:
x=0 và y=m-3
=>OB=|m-3|
Theo đề, ta có: 1/2*(m-3)^2/4=9
=>(m-3)^2/4=18
=>(m-3)^2=72
=>\(m=\pm6\sqrt{2}+3\)
2:
PTHĐGĐ là:
x^2-4x-m+3=0
Δ=(-4)^2-4*(-m+3)=16+4m-12=4m+4
Để (P) cắt (d) tại hai điểm phân biệt thì 4m+4>0
=>m>-1
(4-x1)(x2-1)=2
=>4x2-4-x1x2+1=2
=>x2(x1+x2)-3-(-m+3)=2
=>x2*4-3+m-3=2
=>x2*4=2-m+6=8-m
=>x2=2-1/2m
=>x1=4-2+1/2m=1/2m+2
x1*x2=-m+3
=>-m+3=(1/2m+2)(2-1/2m)=4-1/4m^2
=>-m+3-4+1/4m^2=0
=>1/4m^2-m-1=0
=>m^2-4m-4=0
=>\(m=2\pm2\sqrt{2}\)

14 tháng 7 2023
a: 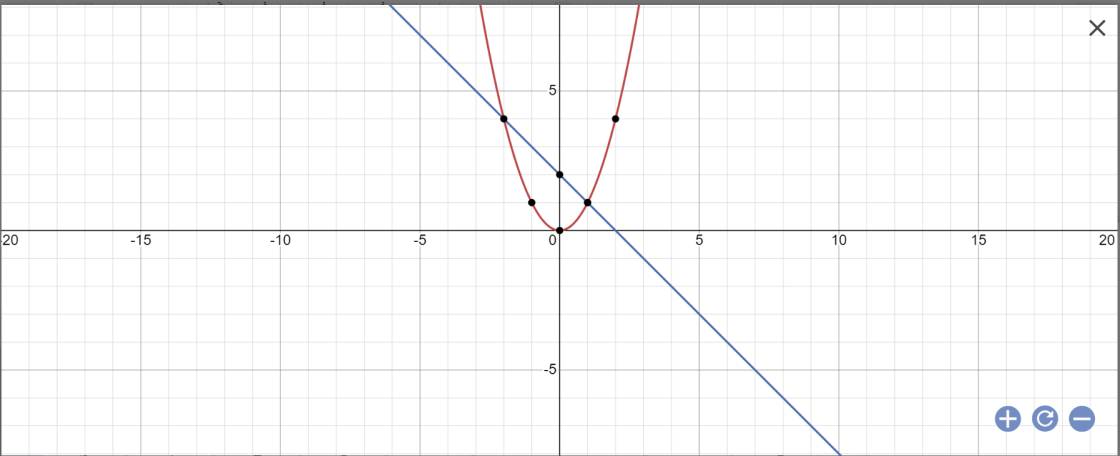
b: PTHĐGĐ là:
x^2+x-2=0
=>(x+2)(x-1)=0
=>x=-2 hoặc x=1
=>y=4 hoặc y=1

a. Bạn tự vẽ nhé, dễ rồi !
b.
Vì A,B là 2 giao điểm của đt (d) với (P) => \(^{x_A,x_B}\)là nghiệm của pt hoành độ giao điểm sau:
\(-\frac{1}{2}x+2=\frac{1}{4}x^2\)
<=> \(\frac{1}{4}x^2+\frac{1}{2}x-2=0\)
<=> \(x^2+2x-8=0\)
<=> \(x^2+2x+1-9=0\)
<=> \(\left(x+1\right)^2-3^2=0\)
\(\Leftrightarrow\left(x+4\right)\left(x-2\right)=0\)
<=> \(\orbr{\begin{cases}x_A=-4\\x_{B=2}\end{cases}}\)
=> \(\hept{\begin{cases}A\left(-4;4\right)\\B\left(2;1\right)\end{cases}}\)
Điểm N thuộc trục hoành => N(n;0)
Ta có: \(NA=\sqrt{\left(x_A-x_N\right)^2+\left(y_A-y_N\right)^2}\)= \(\sqrt{\left(-4-n\right)^2+4^2}=\sqrt{n^2+8n+32}\)
\(NB=\sqrt{(x_B-x_N)^2+\left(y_B-y_N\right)^2}\)= \(\sqrt{\left(2-n\right)^2+1^2}=\sqrt{n^2-4n+5}\)
Tam giác NAB cân tại N <=> NA =NB <=> \(\sqrt{n^2+8n+32}=\sqrt{n^2-4n+5}\)
<=> \(n^2+8n+32=n^2-4n+5\)
<=> \(n=\frac{-27}{12}=\frac{-9}{4}\)
=> \(N\left(\frac{-9}{4};0\right)\)