Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOAM vuông tại A có cosAOM=OA/OM=1/2
nên góc AOM=60 độ
=>sđ cung ANB=gócAOB=2*60=120 độ
b: góc AOB=180-36=144 độ

Bài 7:
a: Xét ΔOAM vuông tại A có
\(\cos\widehat{AOM}=\dfrac{OA}{OM}=\dfrac{1}{2}\)
nên \(\widehat{AOM}=60^0\)
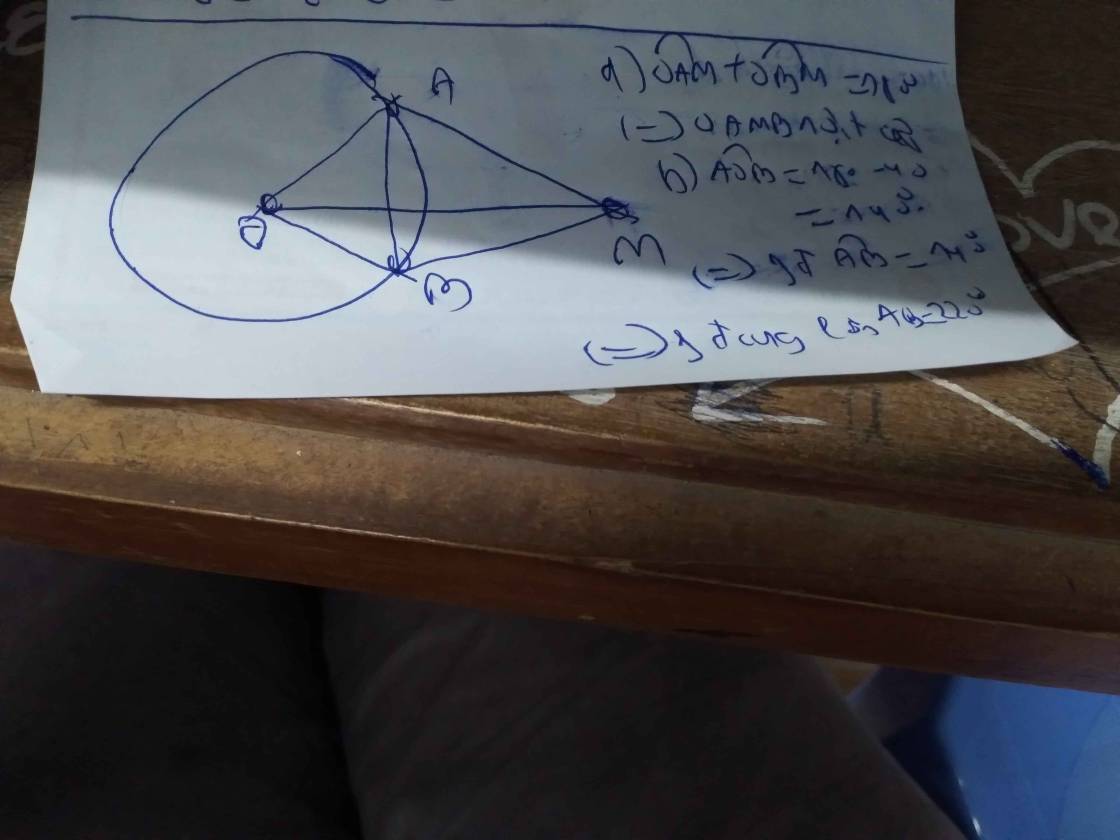
b: Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}=180^0\)
Do đó: OAMB là tứ giác nội tiếp
Suy ra: \(\widehat{AOB}=180^0-36^0=144^0\)

giải b2:
a, MPHQ là hình chữ nhật => MH = PQ
b, Sử dụng hệ thức lượng trong tam giác vuông chứng minh được MP.MA = MQ.MB => ∆MPQ: ∆MBA
c,\(\widehat{PMH}=\widehat{MBH}\Rightarrow\widehat{PQH}=\widehat{O_2QP}\) => PQ là tiếp tuyến của \(\left(O_2\right)\)
Tương tự PQ cũng là tiếp tuyến \(\left(O_1\right)\)

2:
a: góc MAO+góc MBO=180 độ
=>MAOB nội tiếp
b: ΔONP cân tại O
mà OK là trung tuyến
nên OK vuông góc NP
góc OKM=góc OAM=góc OBM=90 độ
=>O,P,A,M,B cùng nằm trên đường tròn đường kính OM
góc AKM=góc AOM
góc BKM=góc BOM
mà góc AOM=góc BOM
nên góc AKM=góc BKM
=>KM là phân giác của góc AKB