Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

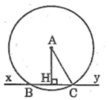
Áp dụng định lí Pitago vào tam giác vuông AHC ta có:
A C 2 = A H 2 + H C 2
Suy ra: H C 2 = A C 2 - A H 2 = 13 2 - 12 2 = 25 => HC = 5 (cm)
Ta có: BC = 2.HC = 2.5 = 10 (cm)

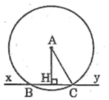
Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C

a, Kẻ OH vuông góc với xy thì OH =12cm <R do đó (O) cắt xy tại hai điểm B,C
b, Tìm được BC = 2, HC = 10cm

a: Kẻ MH vuông góc xy tại H, gọi AB là đường kính của (M)
d(M;xy)=6cm
=>MH=6cm
AB là đường kính của (M)
=>MA=MB=10cm và AB=2*10=20(cm)
Vì MH<MA
nên xy là cát tuyến của (M)
=>(M) cắt xy tại 2 giao điểm
b:
P,Q là 2 giao điểm của (M) với xy
=>MP=MQ=10cm
ΔMPQ cân tại M
mà MH là đường cao
nên H là trung điểm của PQ
ΔMHP vuông tại H
=>\(MP^2=MH^2+HP^2\)
=>\(HP^2=10^2-6^2=64\)
=>HP=8(cm)
H là trung điểm của PQ
=>\(PQ=2\cdot PH=16\left(cm\right)\)

O B C K I A H
a) Xét tam giác vuông ABO có đường cao BK, áp dụng hệ thức lượng trong tam giác ta có:
\(OB^2=OK.OA\Rightarrow5^2=OK.10\Rightarrow OK=2,5\left(cm\right)\)
b) Xét tam giác cân OBC có OK là đường cao nên đồng thời là phân giác.
Vậy thì \(\widehat{BOA}=\widehat{COA}\)
Suy ra \(\Delta ABO=\Delta ACO\left(c-g-c\right)\Rightarrow\widehat{ACO}=\widehat{ABO}=90^o\)
Vậy nên AC là tiếp tuyến của đường tròn (O).
c) Ta thấy ngay \(\Delta KOI\sim\Delta HOA\left(g-g\right)\Rightarrow\frac{OI}{OA}=\frac{OK}{OH}\Rightarrow OI=\frac{OK.OA}{OH}\)
Xét tam giac vuông ABO có BK là đường cao nên áp dụng hệ thức lượng trong tam giác ta có:
\(OK.OA=OB^2=R^2\) không đổi. Lại có OH cũng không đổi (bằng khoảng cách từ O tới đường thẳng xy)
Vậy nên \(OI=\frac{R^2}{OH}\) không đổi.
Vậy khi A di chuyển trên đường thẳng xy thì độ dài đoạn thẳng OI không đổi.

