Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi M(2;1) và d lần lượt là trung điểm và đường trung trực của AB.
Một vectơ pháp tuyến của d là \(\overrightarrow{n}\)=\(\overrightarrow{AB}\)=(2;0).
Phương trình cần tìm:
d: 2.(x-2)+0.(y-1)=0 \(\Rightarrow\) x=2.

Gọi M( 1; 3) là trung điểm của AB.
Ta có ![]()
Gọi d là đường thẳng trung trực của AB thì d qua M( 1;3) và nhận ![]() làm VTCP nên có phương trình tham số là:
làm VTCP nên có phương trình tham số là:

Chọn A.

a) Đường thẳng \(\Delta \) có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\) nên có vectơ chỉ phương \(\overrightarrow u = \left( {5; - 3} \right)\), nên ta có phương trình tham số của \(\Delta \) là :
\(\left\{ \begin{array}{l}x = 1 + 5t\\y = 1 - 3t\end{array} \right.\)
Đường thẳng \(\Delta \) đi qua điểm \(A(1;1)\) và có vectơ pháp tuyến \(\overrightarrow n = \left( {3;5} \right)\)
Phương trình tổng quát của đường thẳng d là:
\(3(x - 1) + 5(y - 1) = 0 \Leftrightarrow 3x + 5y - 8 = 0\)
b) Đường thẳng \(\Delta \) đi qua gốc tọa độ \(O(0;0)\)và có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\), nên có phương trình tham số là:
\(\left\{ \begin{array}{l}x = 2t\\y = - 7t\end{array} \right.\)
Đường thẳng \(\Delta \) có vectơ chỉ phương \(\overrightarrow u = \left( {2; - 7} \right)\),nên có vectơ pháp tuyền là \(\overrightarrow n = \left( {7;2} \right)\) và đi qua \(O(0;0)\)
Ta có phương trình tổng quát là
\(7(x - 0) + 2(y - 0) = 0 \Leftrightarrow 7x + 2y = 0\)
c) Đường thẳng \(\Delta \) đi qua hai điểm \(M(4;0),N(0;3)\) nên có vectơ chỉ phương \(\overrightarrow u = \overrightarrow {MN} = ( - 4;3)\) và có vectơ pháp tuyến \(\overrightarrow n = (3;4)\)
Phương trình tham số của \(\Delta \) là: \(\left\{ \begin{array}{l}x = 4 - 4t\\y = 3t\end{array} \right.\)
Phương trình tổng quát của \(\Delta \) là: \(3(x - 4) + 4(x - 0) = 0 \Leftrightarrow 3x + 4y - 12 = 0\)

Lời giải:
Tọa độ trung điểm của $BC$ là:
\((\frac{x_B+x_C}{2}; \frac{y_B+y_C}{2})=(\frac{3}{2}; \frac{-5}{2})\)
\(B(1,-3); C(2,-2)\Rightarrow \overrightarrow{BC}=(1,1)\)( vecto chỉ phương của $BC$)
Do đường trung trực của $BC$ thì vuông góc với $BC$ nên vecto chỉ phương của đường trung trực chính bằng vecto pháp tuyến của $BC$ và bằng $(-1,1)$
PT tham số của đường trung trực \(\left\{\begin{matrix} x=\frac{3}{2}-t\\ y=\frac{-5}{2}+t\end{matrix}\right.\)
b)
$\Delta$ song song với đt $3x+y-5=0$ nên vecto pháp tuyến của $\Delta$ là \((3,1)\)
Do đó PT tổng quát của $\Delta$ có dạng \(3x+y+k=0\)
$\Delta$ đi qua $A$ nên : \(3.3+5+k=0\Rightarrow k=-14\)
Vậy pt tổng quát của $\Delta$ là \(3x+y-14=0\)

\(AB\left\{{}\begin{matrix}quaA\left(-1;-3\right)\\VTCP\overrightarrow{AB}=\left(-2;8\right)\end{matrix}\right.\)
\(PTTS\) của \(AB:\left\{{}\begin{matrix}x=-1-2t\\y=-3+8t\end{matrix}\right.\)
Gọi \(I\left(x_I;y_I\right)\) là tâm đường tròn
\(I\) là trung điểm \(AB\)
\(\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=\dfrac{-1-3}{2}=-2\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{-3+5}{2}=1\end{matrix}\right.\)
\(\Rightarrow I\left(-2;1\right)\)
\(AB=\sqrt{\left(-2\right)^2+8^2}=2\sqrt{17}\)
Mà \(R=\dfrac{AB}{2}=\dfrac{2\sqrt{17}}{2}=\sqrt{17}\)
Vậy \(PT\left(C\right):\left(x+2\right)^2+\left(y-1\right)^2=17\)

Đáp án: B
Gọi I là trung điểm của AB ⇒ I(0;-1)
A(1;-3), B(-1;1) 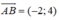
Đường thẳng trung trực của AB là đường thẳng đi qua I và nhận 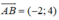 là vecto pháp tuyến: -2(x - 0) + 4(y + 1) = 0 ⇔ x - 2y - 2 = 0
là vecto pháp tuyến: -2(x - 0) + 4(y + 1) = 0 ⇔ x - 2y - 2 = 0

Gọi M trung điểm của AB nên M( 2; 1)
Ta có ![]()
Gọi d là đường thẳng trung trực của AB
thì d qua M(2; 1) và nhận ![]() làm VTPT.
làm VTPT.
Phương trình đường thẳng d là:
1( x- 2) – 6.(y -1) =0
Hay x- 6y+ 4= 0.
Chọn D

a: vecto AB=(2;2)=(1;1)
=>VTPT là (-1;1)
Phương trình tham số AB là: \(\left\{{}\begin{matrix}x=-1+t\\y=0+t=t\end{matrix}\right.\)
Phương trình tổng quát của AB là:
-1(x+1)+1(y-0)=0
=>-x-1+y=0
=>x-y+1=0
b: vecto BC=(2;0)
Vì AH vuông góc BC
nên AH nhận vecto BC làm vtpt và đi qua A
=>AH: 2(x+1)+0(y-0)=0
=>2x+2=0
=>x=-1
c: Tọa độ M la:
x=(-1+3)/2=2/2=1 và y=(0+2)/2=1
B(1;2); M(1;1)
vecto BM=(0;-1)
=>VTPT là (1;0)
Phương trình BM là:
1(x-1)+0(y-2)=0
=>x-1=0
=>x=1
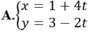
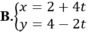
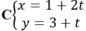
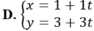




......
\(\overrightarrow{AB}=\left(4;4\right)=4\left(1;1\right)\)
Đường trung trực của AB vuông góc AB nên nhận \(\left(1;-1\right)\) là 1 vtcp
Gọi M là trung điểm AB \(\Rightarrow M\left(1;3\right)\)
Phương trình trung trực AB qua M có dạng: \(\left\{{}\begin{matrix}x=1+t\\y=3-t\end{matrix}\right.\)