Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔBAE và ΔBDE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
b: Xét ΔBFC có
BH là đường cao
BH là đường phân giác
Do đó: ΔBFC cân tại B
=>BF=BC
c: Xét ΔBDF và ΔBAC có
BD=BA
\(\widehat{DBF}\) chung
BF=BC
Do đó: ΔBDF=ΔBAC
=>DF=AC
Ta có: AE+EC=AC
DE+EF=DF
mà AE=DE(ΔBAE=ΔBDE)
và AC=DF
nên EC=EF
Ta có: ΔBAE=ΔBDE
=>\(\widehat{BAE}=\widehat{BDE}\)
=>\(\widehat{BDE}=90^0\)
=>DE\(\perp\)BC
Xét ΔEAF vuông tại A và ΔEDC vuông tại E có
EA=ED
EF=EC
Do đó: ΔEAF=ΔEDC
=>\(\widehat{AEF}=\widehat{DEC}\)
mà \(\widehat{DEC}+\widehat{DEA}=180^0\)(hai góc kề bù)
nên \(\widehat{DEA}+\widehat{AEF}=180^0\)
=>D,E,F thẳng hàng

TA CÓ TAM GIÁC ABC VUÔNG TẠI B , AD ĐL PYTAGO TA CÓ
\(AB^2+BC^2=AC^2\)
=>\(8^2+15^2=289=>AC^{ }=17\)
=>AC=17 CM
A B C E

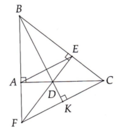
Bạn tự vẽ hình nha
a.
Xét tam giác ABI và tam giác EBI có:
AIB = EIB ( = 900)
BI là cạnh chung
IBA = IBE (BI là tia phân giác của ABE)
=> Tam giác ABI = Tam giác EBI (g.c.g)
=> AB = EB (2 cạnh tương ứng)
b.
Xét tam giác ABD và tam giác EBD có:
BA = BE (theo câu a)
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (c.g.c)
=> BAD = BED (2 góc tương ứng)
mà BAD = 900
=> BED = 900
=> Tam giác BED vuông tại E
c.
BA = BE (theo câu a)
=> Tam giác BAE cân tại B
=> \(BAE=\frac{180^0-ABE}{2}\) (1)
Xét tam giác ADF và tam giác EDC có:
ADF = EDC (2 góc đối đỉnh)
AD = ED (tam giác ABD = tam giác EBD)
FAD = CED ( = 900)
=> Tam giác ADF = Tam giác EDC (g.c.g)
Ta có:
BF = BA + AF
BC = BE + EC
mà BA = BE (theo câu a)
AF = EC (tam giác ADF = tam giác EDC)
=> BF = BC
=> Tam giác BFC cân tại B
=> \(BFC=\frac{180^0-FBC}{2}\) (2)
Từ (1) và (2)
=> BAE = BFC
mà 2 góc này ở vị trí đồng vị
=> AE // FC
Chúc bạn học tốt
A B C F D I E