Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\angle KAC=\angle KBC=90-\angle ACB=\angle HAC\)
mà \(AC\bot HK\Rightarrow\) H và K đối xứng với nhau qua AC
b) Ta có: \(\angle BEM+\angle BDM=90+90=180\Rightarrow BEMD\) nội tiếp
\(\Rightarrow\angle BED=\angle BMD=90-\angle DBM\)
Tương tự \(\Rightarrow MEFC\) nội tiếp \(\Rightarrow\angle FEC=\angle FMC=90-\angle MCA\)
mà \(\angle DBM=\angle MCA\) (ABMC nội tiếp)
\(\Rightarrow\angle BED=\angle CEF\) mà B,E,C thẳng hàng \(\Rightarrow D,E,F\) thẳng hàng
c) Ta có: \(\angle NKM=\angle BKM=\angle BCM=\angle EFM=\angle NFM\)
\(\Rightarrow MFKN\) nội tiếp mà \(MF\parallel NK(\bot AC)\)
\(\Rightarrow MFKN\) là hình thang cân \(\Rightarrow\angle MNH=\angle FKH=\angle FHK\) (K và H đối xứng qua AC)
\(\Rightarrow HF\parallel NM\) mà \(FM\parallel NH\) \(\Rightarrow MNHF\) là hình bình hành
có MN và HF là 2 đường chéo cắt nhau tại I
\(\Rightarrow I\) là trung điểm MH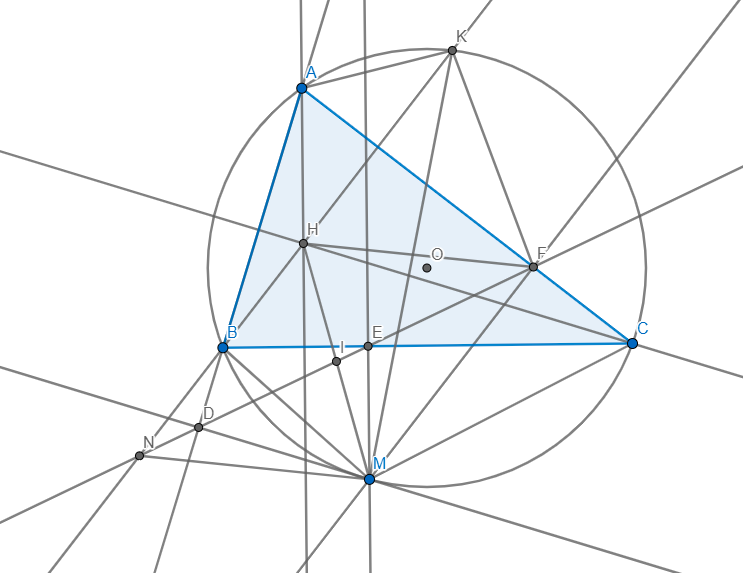

a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

Em không vẽ được hình, xin thông cảm
a, Ta có góc EAN= cungEN=cung EC+ cung EN
Mà cung EC= cung EB(E là điểm chính giữa cung BC)
=> góc EAN=cungEB+ cung EN=góc DFE (tính chất góc ở giữa)
=> tam giác AEN đồng dạng tam giác FED
Vậy tam giác AEN đồng dạng tam giác FED
b,Ta có EC=EB=EM
Tam giác EMC cân tại E => EMC=ECM
MÀ EMC+AME=180, ECM+ABE=180
=> AME = ABE
=> tam giác ABE= tam giác AME
=> AB=AM => tam giác ABM cân tại A
Mà AE là phân giác => AE vuông góc BM
CMTT => AC vuông góc EN
MÀ AC giao BM tại M
=> M là trực tâm tam giác AEN
Vậy M là trực tâm tam giác AEN
c, Gọi H là giao điểm OE với đường tròn (O) (H khác E) => O là trung điểm của EH
Vì M là trực tâm của tam giác AEN
=> \(EN\perp AN\)
Mà \(OI\perp AN\)(vì I là trung điểm của AC)
=> \(EN//OI\)
MÀ O là trung điểm của EH
=> I là trung điểm của MH (đường trung bình trong tam giác )
=> tứ giác AMNH là hình bình hành
=> AH=MN
Mà MN=NC
=> AH=NC
=> cung AH= cung NC
=> cung AH + cung KC= cung KN
Mà cung AH+ cung KC = góc KMC(tính chất góc ở giữa 2 cung )
NBK là góc nội tiếp chắn cung KN
=> gócKMC=gócKBN
Hay gócKMC=gócKBM
=> CM là tiếp tuyến của đường tròn ngoại tiếp tam giác MBK( ĐPCM)
Vậy CM là tiếp tuyến của đường tròn ngoại tiếp tam giác BMK

O A B C M K H E d P F I
1) Dễ thấy \(\widehat{HCB}=\widehat{ACB}=90^o\)
tứ giác CBKH có \(\widehat{HKB}=\widehat{HCB}=90^o\)nên là tứ giác nội tiếp
\(\Rightarrow\widehat{HCK}=\widehat{HBK}\)( 1 )
Mà \(\widehat{ACM}=\widehat{ABM}=\frac{1}{2}sđ\widebat{AM}\)( 2 )
Từ ( 1 ) và ( 2 ) suy ra \(\widehat{ACM}=\widehat{ACK}\)
2) Xét \(\Delta AMC\)và \(\Delta BEC\)có :
AM = BE ; AC = BC ; \(\widehat{MAC}=\widehat{CBE}=\frac{1}{2}sđ\widebat{MC}\)
\(\Rightarrow\Delta AMC=\Delta BEC\)( c.g.c )
\(\Rightarrow MC=EC\)
Ta có : \(\widehat{CMB}=\frac{1}{2}sđ\widebat{BC}=45^o\)
Suy ra \(\Delta ECM\)vuông cân tại C
3) Ta có : \(\frac{AP.MB}{AM}=R=OB\Rightarrow\frac{AP}{MA}=\frac{OB}{MB}\)
Xét \(\Delta APM\)và \(\Delta OBM\), ta có :
\(\frac{AP}{MA}=\frac{OB}{MB}\); \(\widehat{PAM}=\widehat{MBO}=\frac{1}{2}sđ\widebat{AM}\)
\(\Rightarrow\Delta APM\approx\Delta BOM\left(c.g.c\right)\)
\(\Rightarrow\Delta APM\)cân tại P ( vì \(\Delta BOM\)cân tại O )
\(\Rightarrow PA=PM\)
Gọi giao điểm của BM và ( d ) là F ; giao điểm của BP với HK là I
Xét tam giác vuông AMF có PA = PM nên PA = PM = PF
Theo định lí Ta-let, ta có :
\(\frac{HI}{FP}=\frac{BI}{BP}=\frac{KI}{AP}\Rightarrow HI=KI\)
vì vậy PB đi qua trung điểm của HK
