Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 4 số cần tìm là \(a_1,a_2,a_3,a_4\). Theo đầu bài ta có hệ :
\(\begin{cases}a_2^2=a_1a_3\\2a_3=a_2+a_4\\a_1+a_4=14\\a_2+a_3=12\end{cases}\) \(\Leftrightarrow\begin{cases}2a_1q^2=a_1q+a_2+d\left(1\right)\\a_1+a_2+d=14\left(2\right)\\a_1q+a_1q^2=12\left(3\right)\\a_2+a_2+d=12\left(4\right)\end{cases}\)
\(\Leftrightarrow\begin{cases}a_2^2=a_1\left(a_2+d\right)\left(5\right)\\a_2+2d=14-a_1\\a_1=\frac{12}{q+q^2}\\d=12-2a_2\end{cases}\)
Giải hệ thống các phương trình ta có kết quả \(\left(2,4,8,12\right)\left(\frac{25}{2},\frac{15}{2}\frac{9}{2}\frac{3}{2}\right)\)

Chọn B.
Gọi bốn số đó là a ;b ;c ;d ta có hệ:
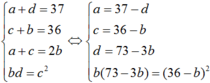
Giải ra ta được : b = 16 ; c = 20 ; d = 25 ; a = 12.

+ Gọi số hạng đầu của cấp số nhân là u1, công bội là x
Theo giả thiết ta có hệ phương trình
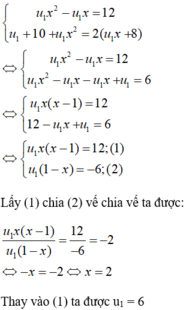
+ Tổng của năm số hạng đầu của CSN là:


Theo giả thiết ta có :
\(u_1+u_2=u_1+\frac{1}{4}\left(u_1\right)=24\)
\(\Rightarrow u_1+\frac{1}{4}u_1^2-24=0\)
\(\Leftrightarrow u_1=-12\) V \(u_1=8\)
Vậy có 2 cấp số nhân tương ứng là : 8,16,32,128 hoặc -12,36,-108,-972

Gọi công bội của cấp số nhân là q => b=a.q; c=a.q^2
Gọi công sai của cấp số cộng là d => b=a+2d; c=a+8d
Ta có: a.q=a+2d => \(q=\dfrac{a+2d}{a}=1+2\dfrac{d}{a}\)
\(a.q^2=a+8d\Rightarrow q^2=\dfrac{a+8d}{a}=1+8\dfrac{d}{a}\)
Suy ra \(\left(1+2\dfrac{d}{a}\right)^2=1+8\dfrac{d}{a}\Rightarrow\dfrac{d}{a}=1\left(d\ne0\right)\)
=> b=a+2a=3a; c=a+8a=9a
Theo bài ra a+b+c=26 => a+3a+9a=13a=26 => a=2; b=6; c=18
Vậy ba số cần tìm là a=2; b=6; c=18
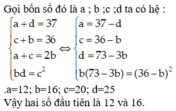
Chọn D
Gọi 4 số phải tìm là a1, a2, a3, a4. Theo đầu bài Ta có hệ:
Giải các hệ phương trình Ta có kết quả a1=2, a2=4, a3=8 và a4=12
Chọn D