Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

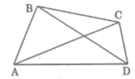
Có bốn tam giác thỏa mãn yêu cầu đề bài, tên các tam giác đó là:
Tam giác ABC, tam giác CAD, tam giác BCD và tam giác ABD

Ta có hình vẽ
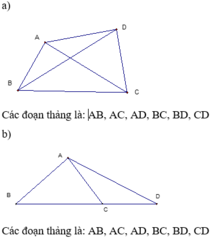
Có tất cả 10 hình tam giác đó là ABC,ACD,ADE,AEB,BEC,BCD,BED,CED,CEA,DAB

nếu k có 4 điểm thẳng hàng thì ta có:
100x99:2=4950 (đường thẳng)
do có 4 điểm thẳng hàng nên ta chỉ vẽ đc 1 đường thẳng với 4 điểm đó
=> Có tất cả :
4950-(1x4)=4946 ( đường thẳng)
d/s:.....
Nếu không có 4 điểm thẳng hàng thì ta có:
100 x 99 : 2 = 4950 ( đường thẳng )
Do có 4 điểm thẳng hàng nên ta chỉ vẽ đươccj 1 đường thẳng với 4 điểm đó.
Có tất cả số đường thẳng là:
4950 - ( 1 x 4 ) = 4946 ( đường thẳng )
Đáp số: 4946 đường thẳng

Đáp án là B
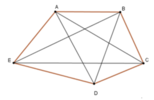
Có 10 tam giác mà các đỉnh là ba trong năm điểm đã cho là:
ΔABC; ΔABD; ΔABE; ΔBCD; ΔBCE; ΔCDA; ΔCDE; ΔDEB; ΔDEA; ΔAEC

Có tất cả 4 tam giác :
\(\Delta\)ABC
\(\Delta\)BCD
\(\Delta\)CDA
\(\Delta\)ABD