Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

-Gọi số công nhân hoàn thành công việc trong 14 ngày là x (x€ N*) (công nhân)
- Vì số công nhân làm việc và số thời gian để hoàn thành công việc là 2 đại lượng tỷ lệ nghịch nên ta có:
56. 21= x. 14
=>1176 = x. 14
x= 1176 : 14
x= 84 (công nhân).
=> Số công nhân tăng thêm để hoàn thành công việc trong 14 ngày là:
84 - 56 = 28 (công nhân)
Vậy phải tăng thêm 28 công nhân để hoàn thành công việc trong 14 ngày.

Gọi số công nhân hoàn thành công việc trong 14 ngày là a(\(a\in N\)*)
Vì trong cùng một công việc thời gian và số người hoàn thành là hai đại lượng tỉ lệ nghịch nên ta có:
\(56\cdot21=14a\)
\(a=\frac{56\cdot21}{14}\)
\(a=84\)
Số công nhân cần phải tăng thêm là:
84-56=28(công nhân)
Vậy cần phải tăng thêm 28 công nhân

Gọi số công nhân hoàn thành công việc đó trong 14 ngày là x (người) với x \(\in\) N*
Với cùng 1 khối lượng công việc, số người làm công việc đó và số ngày làm xong công việc là 2 đại lượng tỉ lệ nghịch nên ta có : \(\frac{x}{56}=\frac{21}{14}\)
\(\Rightarrow x=\frac{21}{14}.56=84\)
Số người cần tăng thêm để hoàn thành công việc đó trong 14 ngày là :
84 - 56 = 28 (người)
tóm tắt :
56 công nhân làm trong 21 ngày
x công nhân làm trong 14 ngày
giải :
vì số công nhân và thời gian là hai đại lượng tỉ lệ nghịch
=>\(\frac{56}{x}=\frac{14}{21}\)
=>\(x=\frac{21.56}{14}=84\)(công nhân )
=>cần thêm số công nhân là :
84-56=28 công nhân
đ/s...

Gọi số công nhân để hoàn thành công việc trong 14 ngày là a (công nhân, a 
Vì số công nhân và số ngày là hai đại lượng tỉ lệ nghịch
\(\Rightarrow\frac{56}{a}=\frac{14}{21}\)\(\Rightarrow a=\frac{56.21}{14}=84\)
=> Cần 84 công nhân để hoàn thành công việc trong 14 ngày
=> Cần phải tăng thêm số công nhân nữa để có thể hoàn thành công việc đó trong 14 ngày là: 84 - 56 = 28 (công nhân)
Vậy cần phải tăng thêm 28 công nhân nữa để có thể hoàn thành công việc đó trong 14 ngày.

Cần phải tăng thêm:
\(\left|56\cdot24:14-56\right|=40\left(người\right)\)
Lời giải:
Vì số công nhân và số ngày hoàn thành công việc là 2 đại lượng tỉ lệ nghịch ( càng nhiều người thì thời gian xong việc càng ngắn) nên để hoàn thành công việc trong 14 ngày cần số người là:
$56.24:14=96$ (người)
Cần tăng thêm số công nhân là:
$96-56=40$ (người)

Gọi x là số công nhân làm xong công việc trong 14 ngày
Vì năng suất các công nhân là như nhau nên số công nhân và số ngày làm xong công việc là hai đại lượng tỉ lệ nghịch nên ta có:
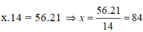
Vậy để hoàn thành công việc đó trong 14 ngày thì cần 84 công nhân. Do đó số người cần tăng thêm là 84 – 56 = 28 người.
 cao nguyễn thu uyên
cao nguyễn thu uyên
Vì mỗi công nhân năng suất như nhau và cùng hoàn thành chung 1 công việc nên số công nhân(x) tỉ lệ nghịch với số thời gian hoàn thành(y) nên \(\frac{x_1}{x_2}=\frac{y_2}{y_1}\) hay \(\frac{56}{x_2}=\frac{14}{21}\)
=>x2=56:14/21=84
=>x2-x1=84-56=28
Vậy phải tăng thêm 28 công nhân nữa để hoàn thành công việc trong 14 ngày