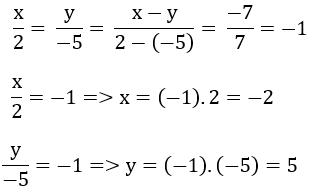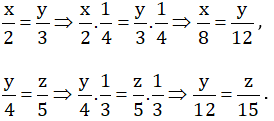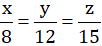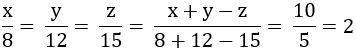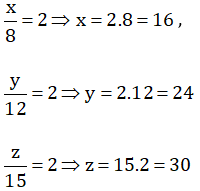Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gợi ý nhá
Bài 3: câu 1: làm tương tự như câu hỏi lần trước bạn gửi.
b) Bạn chỉ cần cho tử và mẫu mũ 3 lên. theé là dễ r
\(\frac{x^3}{8}=\frac{y^3}{64}=\frac{z^3}{216}\Rightarrow=\frac{x}{2}=\frac{y}{4}=\frac{z}{6}\Rightarrow=\frac{x^2}{4}=\frac{y^2}{16}=\frac{z^2}{36}\)
áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{x^2}{4}=\frac{y^2}{16}=\frac{z^2}{36}=\frac{x^2+y^2+z^2}{4+16+36}=\frac{14}{56}=\frac{1}{4}\)
tự tính tiếp =)


\(\frac{x}{2}=\frac{y}{3};\frac{y}{4}=\frac{z}{5}\)
=> \(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}\) (x+y-z=10)
Theo tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{8}=\frac{y}{12}=\frac{z}{15}=\frac{x+y-z}{8+12-15}=\frac{10}{5}=2\)
\(\hept{\begin{cases}\frac{x}{8}=2\Rightarrow x=2.8=16\\\frac{y}{12}=2\Rightarrow y=2.12=24\\\frac{z}{15}=2\Rightarrow z=2.15=30\end{cases}}\)
Vậy x=16 ; y=24 và z=30

\(\frac{a}{3}=\frac{b}{2};\frac{b}{7}=\frac{c}{5}\)
Vì \(\frac{a}{3}=\frac{b}{2};\frac{b}{7}=\frac{c}{5}\)
=> \(\frac{a}{3}=\frac{b}{2}\Rightarrow\frac{a}{21}=\frac{b}{14}\)(1)
\(\frac{b}{7}=\frac{c}{5}\Rightarrow\frac{b}{14}=\frac{c}{10}\)(2)
Từ (1) và (2) \(\Rightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\Rightarrow\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}\)
Theo tính chất dãy tỉ số bằng nhau:
\(\Rightarrow\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}\Rightarrow\frac{3a-7b+5c}{63-98+50}=\frac{30}{15}=2\)
Do đó: \(\Rightarrow\hept{\begin{cases}\frac{a}{21}=2\Rightarrow a=42\\\frac{b}{14}=2\Rightarrow b=28\\\frac{c}{10}=2\Rightarrow c=20\end{cases}}\)
Vậy: a = 42
b = 28
c = 20
Bài 1:
a)
Ta có: \(\frac{a}{3}=\frac{b}{2}\)
\(\Rightarrow\frac{a}{3}.\frac{1}{7}=\frac{b}{2}.\frac{1}{7}\)
\(\Rightarrow\frac{a}{21}=\frac{b}{14}\)
Và: \(\frac{b}{7}=\frac{c}{5}\)
=> \(\frac{b}{7}.\frac{1}{2}=\frac{c}{5}.\frac{1}{2}\)
=> \(\frac{b}{14}=\frac{c}{10}\)
Do đó: \(\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)
Áp dụng tính chất dãy tỉ số bằng nhau; ta có:
\(\frac{a}{21}=\frac{b}{14}=\frac{c}{10}\)\(=\frac{3a}{63}=\frac{7b}{98}=\frac{5c}{50}=\frac{3a-7b-5c}{63-98-50}\)\(=\frac{30}{-85}\)\(=-\frac{6}{17}\)
+) Với \(\frac{a}{21}=-\frac{6}{17}\Rightarrow a=-\frac{126}{17}\)
+) Với \(\frac{b}{14}=-\frac{6}{17}\Rightarrow b=-\frac{84}{17}\)
+)Với \(\frac{c}{10}=-\frac{6}{17}\Rightarrow c=-\frac{60}{17}\)
Vậỵ:..........
b)
Ta có: 7a = 9b = 21c
=> 7a/63 = 9b/63 = 21c/63
=> a/9 = b/7 = c/3
Áp dụng tính chất dãy tỉ số bằng nhau; ta có:
a/9 = b/7 = c/3 = (a-b+c) / (9-7+3) = -15/5 = -3
+) a/9 = -3 => a = -27
+) b/7 = -3 => b = -21
+) c/3 = -3 => c = -9
Vậy:..............
Bài 2:
a) Theo bài: x:y:z = 5:3:4
=> x/5 = y/3 = z/4
Áp dụng tính chất dãy tiwr số bằng nhau; ta có:
x/5 = y/3 = z/4 = ( x + 2y -z ) / ( 5 + 2.5 - 4 ) = -121 / 11 = -11
+) Với x/5 = -11 => x=-55
+) Với y/3 = -11 => y = -33
+) Với z/4 = -11 => z = -44
Vậy:......
b) _ Tương tự câu a) ở bài 1
c)
Ta đặt: x/3 = y/12 = z/5 = k ( \(k\inℤ\))
=> \(\hept{\begin{cases}x=3k\\y=12k\\z=5k\end{cases}}\)
Theo bài: xyz = 22,5
=> 3k.12k.5k = 22,5
=> 180.k3 = 22,5
=> k3 = 1/8 = (1/2)3
=> k = 1/2
Với k = 1/2 => x = 3/2; y = 6; z = 5/2
Vậy:..........
d)

a) Ta có: \(x:2=y:\left(-5\right)\)
nên \(\dfrac{x}{2}=\dfrac{y}{-5}\)
mà x-y=-7
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{2}=\dfrac{y}{-5}=\dfrac{x-y}{2-\left(-5\right)}=\dfrac{-7}{7}=-1\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{2}=-1\\\dfrac{y}{-5}=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=5\end{matrix}\right.\)
Vậy: (x,y)=(-2;5)
b) Ta có: \(\dfrac{x}{2}=\dfrac{y}{3}\)
nên \(\dfrac{x}{8}=\dfrac{y}{12}\)(1)
Ta có: \(\dfrac{y}{4}=\dfrac{z}{5}\)
nên \(\dfrac{y}{12}=\dfrac{z}{15}\)(2)
Từ (1) và (2) suy ra \(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}\)
mà x+y-z=10
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{8}=\dfrac{y}{12}=\dfrac{z}{15}=\dfrac{x+y-z}{8+12-15}=\dfrac{10}{5}=2\)
Do đó:
\(\left\{{}\begin{matrix}\dfrac{x}{8}=2\\\dfrac{y}{12}=2\\\dfrac{z}{15}=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=16\\y=24\\z=30\end{matrix}\right.\)
Vậy: (x,y,z)=(16;24;30)
b)
Do đó ta có
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:

\(\frac{x}{12}=\frac{y}{9}=\frac{z}{5}\)và\(x\cdot y\cdot z=20\)
Đặt \(\frac{x}{12}=\frac{y}{9}=\frac{z}{5}=K\)
\(\Rightarrow\frac{x}{12}=K\Rightarrow x=12K\)
\(\Rightarrow\frac{y}{9}=K\Rightarrow y=9K\)
\(\Rightarrow\frac{z}{5}=K\Rightarrow z=5K\)
Mà \(12K\cdot9K\cdot5K=20\)
\(\Rightarrow\left(12\cdot9\cdot5\right)\cdot K=20\)
\(\Rightarrow540k=20\)
\(\Rightarrow K=20:540\)
\(\Rightarrow K=+-\frac{1}{27}\)
KHi đó \(\frac{x}{12}=\frac{1}{27}\Rightarrow x=\frac{4}{9}\)
\(\frac{y}{9}=\frac{1}{27}\Rightarrow y=\frac{1}{3}\)
\(\frac{z}{5}=\frac{1}{27}\Rightarrow z=\frac{5}{27}\)
Còn lại bn lm tương tự ha
Đặt \(\frac{x}{12}\)=\(\frac{y}{9}\)=\(\frac{z}{5}\)=k
-->x=12k;y=9k;z=5k
-->12k.9k.5k=20
-->12.9.5.k3=20
-->540.k3=20
-->k3=\(\frac{1}{27}\)-->k=\(\frac{1}{3}\)
-->x=\(\frac{1}{3}\).12=4
y=\(\frac{1}{3}\).9=3
z=\(\frac{1}{3}\).5=\(\frac{5}{3}\)
Vậy x=4;y=3;z=\(\frac{5}{3}\)

Bài 1:
Gọi độ dài các cạnh của tam giác đó lần lượt là x;y;z ( x;y;z > 0)
Ta có: \(\frac{x}{4}=\frac{y}{7}=\frac{z}{5};x+y+z=48\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{x}{4}=\frac{y}{7}=\frac{z}{5}=\frac{x+y+z}{4+7+5}=\frac{48}{16}=3\)
\(\Rightarrow\frac{x}{4}=3\Rightarrow x=3.4=12\)
\(\frac{y}{7}=3\Rightarrow y=3.7=21\)
\(\frac{z}{5}=3\Rightarrow z=3.5=15\)
Vậy độ dài các cạnh của tam giác đó lần lượt là: 12;21;15
thank trc ^~^