Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

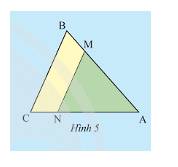
a) Ta có: \(\frac{{A'B'}}{{AB}} = \frac{2}{6} = \frac{1}{3},\frac{{A'C'}}{{AC}} = \frac{3}{9} = \frac{1}{3},\frac{{B'C'}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\). Do đó, các tỉ số trên bằng nhau.
b) Ta có: \(\frac{{AM}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AN}}{{AC}} = \frac{3}{9} = \frac{1}{3}\)
Vì \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} \Rightarrow MN//BC\) (định lí Thales đảo)
Vì \(MN//BC \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (Hệ quả của định lí Thales)
Do đó, \(\frac{{MN}}{{BC}} = \frac{1}{3} \Leftrightarrow \frac{{MN}}{{12}} = \frac{1}{3} \Rightarrow MN = \frac{{12.1}}{3} = 4\).
Vậy \(MN = 4cm\).
c) Vì \(MN//BC \Rightarrow \Delta ABC\backsim\Delta AMN\) (định lí)(1)
Xét tam giác \(AMN\) và tam giác \(A'B'C'\) ta có:
\(AM = A'B' = 2cm;AN = A'C' = 2cm;MN = B'C' = 4cm\)
Do đó, \(\Delta AMN = \Delta A'B'C'\) (c.c.c)
Vì \(\Delta AMN = \Delta A'B'C'\) nên \(\Delta AMN\backsim\Delta A'B'C'\) (2)
Từ (1) và (2) suy ra, \(\Delta ABC\backsim\Delta A'B'C'\).

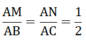
⇒ MN // BC (định lí Ta lét đảo)
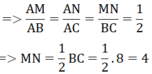
Suy ra: Δ AMN = ∆ A’B’C’(c.c.c) nên hai tam giác này cũng đồng dạng với nhau (1).
Xét tam giác ABC có MN// BC nên Δ AMN đồng dạng với tam giác ABC (2)
Từ (1) và (2) suy ra: Δ A’B’C’ đồng dạng với tam giác ABC (tính chất).

a: Xét ΔBAC vuông tại B và ΔB'A'C' vuông tại B' có
góc C=goc C'
=>ΔBAC đồng dạng vói ΔB'A'C'
b: ΔBAC đồng dạng với ΔB'A'C'
=>BA/B'A'=AC/A'C'=BC/B'C'
=>A'C'/5=B'C'/4=6/3=2
=>A'C'=10cm; B'C'=8cm

Vì \(MN//BC\) nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\) (các cặp góc đồng vị)
Xét tam giác \(ABC\) có, \(MN//BC\) nên theo hệ quả của định lí Thales ta có:
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Vậy trong các ô trống cần điền là:
\(\widehat A\) chung;
\(\widehat M = \widehat B\);
\(\widehat N = \widehat C\);
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\).
Tam giác \(\Delta AMN\) và\(\Delta ABC\) có các góc tương ứng bằng nhau và tỉ số các cạnh tương ứng bằng nhau nên \(\Delta AMN\) đồng dạng \(\Delta ABC\).
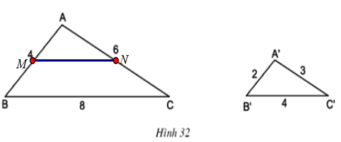

Bổ sung đề: AB=6cm; AC=9cm
a: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
b: Ba tam giác này đồng dạng với nhau