VN
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
7 tháng 5 2019
Ta có: x + y = ( a 1 2 + b 1 ) + ( a 2 2 + b 2 ) = ( a 1 + a 2 ) 2 + ( b 1 + b 2 )
Vì a 1 , a 2 , b 1 , b 2 là các số hữu tỉ nên a 1 + a 2 , b 1 + b 2 cũng là số hữu tỉ.
Lại có: xy = ( a 1 2 + b 1 )( a 2 2 + b 2 ) = 2 a 1 a 2 + a 1 b 2 2 + a 2 b 1 2 + b 1 b 2
= ( a 1 b 2 + a 2 b 1 ) 2 + (2 a 1 a 2 + b 1 b 2 )
Vì a 1 , a 2 , b 1 , b 2 là các số hữu tỉ nên a 1 b 2 + a 2 b 1 , a 1 a 2 + b 1 b 2 cũng là các số hữu tỉ.
CM
22 tháng 6 2018
Ta chứng minh BĐT
( a + b + c ) ( 1 a + 1 b + 1 c ) ≥ 9 ( * ) ( * ) < = > 3 + ( a b + b a ) + ( b c + c b ) + ( c a + a c ) ≥ 9
Áp dụng BĐT Cô – si cho hai số dương ta có:
a b + b a ≥ 2 b c + c b ≥ 2 c a + a c ≥ 2 =>(*) đúng
= > 9 a + b + c ≤ 1 a + 1 b + 1 c ≤ 3 = > a + b + c ≥ 3
Trở lại bài toán: Áp dụng BĐT Cô si cho hai số dương ta có 1 + b 2 ≥ 2 b
Ta có: a 1 + b 2 = a − a b 2 1 + b 2 ≥ a − a b 2 2 b = a − a b 2 ( 1 )
Tương tự ta có:
b 1 + c 2 ≥ b − b c 2 ( 2 ) c 1 + a 2 ≥ c − c a 2 ( 3 )
Cộng từng vế của (1), (2) và (3) ta có:
a 1 + b 2 + b 1 + c 2 + c 1 + a 2 ≥ a + b + c − 1 2 ( a b + b c + c a ) = > a 1 + b 2 + b 1 + c 2 + c 1 + a 2 + 1 2 ( a b + b c + c a ) ≥ a + b + c ≥ 3
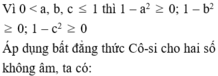
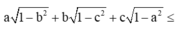
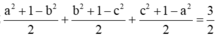
Dễ vậy mà ko làm đc àk
\(a_1.a_2=b_1.b_2\Rightarrow\frac{a_1}{b_1}=\frac{b_2}{a_2}\)
\(\Rightarrow\frac{a_1}{b_1}+\frac{a_2}{b_2}=\frac{b_2}{a_2}+\frac{a_2}{b_2}\ge2\sqrt{\frac{b_2}{a_2}.\frac{a_2}{b_2}}=2\) (AM - GM)
có a1.a2=b1.b2
=> a1/b1=b2/a2
có \(\frac{a1}{b1}+\frac{a2}{b2}=\frac{b2}{a2}+\frac{a2}{b2}\)
áp dụng bất đẳng thức cosi cho 2 số dương có
\(\frac{b2}{a2}+\frac{a2}{b2}\ge2\sqrt{\frac{b2}{a2}.\left(\frac{a2}{b2}\right)}=2\)(đpcm)