Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Để hai đường song song thì
\(\left\{{}\begin{matrix}2m^2-m=1\\m^2+m< >2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m-1\right)\left(2m+1\right)=0\\\left(m+2\right)\left(m-1\right)< >0\end{matrix}\right.\Leftrightarrow m=-\dfrac{1}{2}\)
b: Thay x=2 vào (d1), ta đc:
\(y=2+2=4\)
Vì (d3) vuông góc với (d1) nên (d3): y=-x+b
Thay x=2 và y=4 vào (d3), ta được:
b-2=4
=>b=6

a: Tọa độ A là: x=4 và y=x=4
Tọa độ B là 3x=4 và y=4
=>x=4/3 và y=4
b: \(OA=\sqrt{\left(4-0\right)^2+\left(4-0\right)^2}=4\sqrt{2}\)
\(OB=\sqrt{\left(\dfrac{4}{3}\right)^2+4^2}=\dfrac{4\sqrt{10}}{3}\left(cm\right)\)
\(AB=\sqrt{\left(\dfrac{4}{3}-4\right)^2+\left(4-4\right)^2}=\dfrac{8}{3}\left(cm\right)\)
=>\(p=\dfrac{1}{2}\left(4\sqrt{2}+\dfrac{4}{3}\sqrt{10}+\dfrac{8}{3}\right)=2\sqrt{2}+\dfrac{2}{3}\sqrt{10}+\dfrac{4}{3}\left(cm\right)\)
=>S=16/3

a/ Hoành độ giao điểm của (d1) và (d3) là nghiệm của phương trình:
x = 4 => y = 4
Vậy tọa độ giao điểm A của (d1) và (d3) là A(4 ; 4)
Hoành độ giao điểm của (d2) và (d3) là nghiệm của phương trình:
3x = 4 <=> x = 4/3 => y = 4
Vậy tọa độ giao điểm B của (d2) và (d3) là B(4/3; 4)
b/ độ dài đt : \(AB=\sqrt{\left(x_B-x_A\right)^2+\left(y_B-y_A\right)^2}=\sqrt{\left(\dfrac{4}{3}-4\right)^2+\left(4-4\right)^2}=\dfrac{8}{3}\left(cm\right)\)
Gọi OH là đường cao của tam giác OAB và OH cũng chính là đt d3 :
\(S_{OAB}=\dfrac{1}{2}.\dfrac{8}{3}.4=\dfrac{16}{3}\left(cm^2\right)\)
Vậy ...
a/ Hoành độ giao điểm của (d1) và (d2) là nghiệm của phương trình:
x = 4 => y = 4
Vậy tọa độ giao điểm A của (d1) và (d2) là E(4 ; 4)
Hoành độ giao điểm của (d2) và (d3) là nghiệm của phương trình:
3x = 4 <=> x = 4/3 => y = 4
Vậy tọa độ giao điểm A của (d1) và (d2) là E(4/3; 4)
b/ điểm B ????

Lời giải:
a) Gọi tọa độ giao điểm $(d_1)$ và $(d_3)$ là $A(x_0, y_0)$
Vì \(A\in (d_1), (d_3)\Rightarrow \left\{\begin{matrix} y_0=x_0\\ y_0=4\end{matrix}\right.\)
\(\Rightarrow x_0=y_0=4\Rightarrow A(4;4)\)
-----------
Gọi $B(x_0,y_0)$ là giao điểm của $(d_2)$ và $(d_3)$
\(\Rightarrow \left\{\begin{matrix} y_0=3x_0\\ y_0=4\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_0=\frac{4}{3}\\ y_0=4\end{matrix}\right.\)
Vậy \(B(\frac{4}{3}; 4)\)
b) Ta có:
\(AB=\sqrt{(\frac{4}{3}-4)^2+(4-4)^2}=\frac{8}{3}\)
Gọi $H$ là giao điểm của $(d_3)$ với trục tung $Oy$
Khi đó \(H(0;4)\)
\(d(O, AB)=OH=|y_H|=4\)
Do đó: \(S_{AOB}=\frac{OH.AB}{2}=\frac{4.\frac{8}{3}}{2}=\frac{16}{3}\) (đơn vị diện tích)

a: Tọa độ A là: x=4 và y=x=4
Tọa độ B là 3x=4 và y=4
=>x=4/3 và y=4
b: \(OA=\sqrt{\left(4-0\right)^2+\left(4-0\right)^2}=4\sqrt{2}\)
\(OB=\sqrt{\left(\dfrac{4}{3}\right)^2+4^2}=\dfrac{4\sqrt{10}}{3}\left(cm\right)\)
\(AB=\sqrt{\left(\dfrac{4}{3}-4\right)^2+\left(4-4\right)^2}=\dfrac{8}{3}\left(cm\right)\)
=>\(p=\dfrac{1}{2}\left(4\sqrt{2}+\dfrac{4}{3}\sqrt{10}+\dfrac{8}{3}\right)=2\sqrt{2}+\dfrac{2}{3}\sqrt{10}+\dfrac{4}{3}\left(cm\right)\)
=>S=16/3

a: Tọa độ A là:
\(\left\{{}\begin{matrix}-x+5=\dfrac{1}{4}x\\y=\dfrac{1}{4}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{5}{4}x=-5\\y=\dfrac{1}{4}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=1\end{matrix}\right.\)
Tọa độ B là:
-x+5=4x và y=4x
=>-5x=-5 và y=4x
=>B(1;4)
Tọa độ C là:
1/4x=4x và y=4x
=>C(0;0)
b: A(4;1); B(1;4); O(0;0)
\(OA=\sqrt{4^2+1^2}=\sqrt{17}\)
\(OB=\sqrt{4^2+1^2}=\sqrt{17}\)
=>OA=OB
=>ΔOAB cân tại O
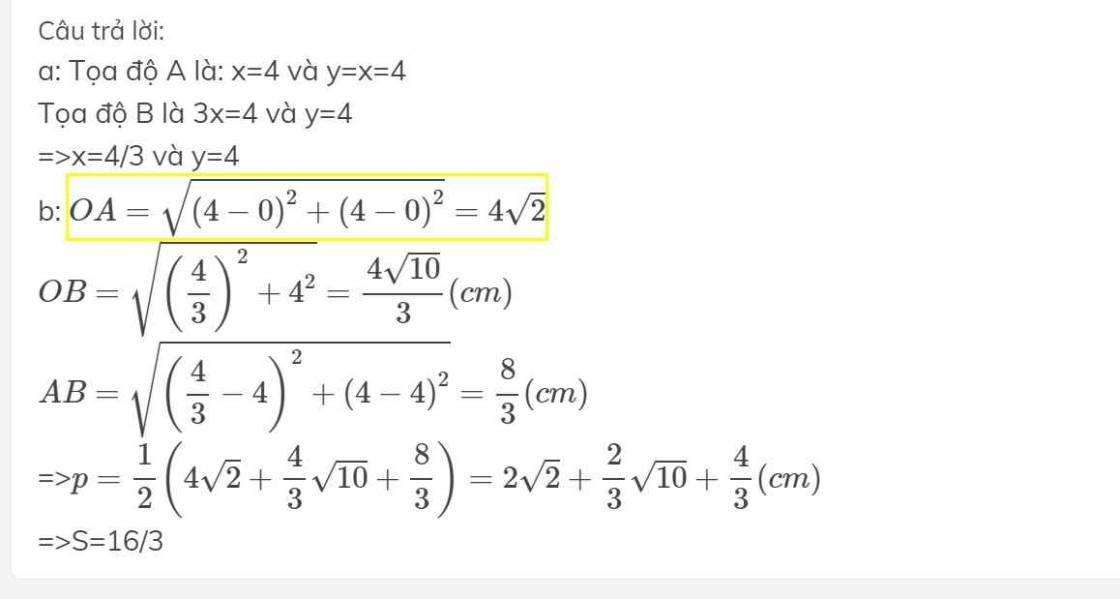

b: Vì (d1)//(d3) nên a=1
hay (d1): y=x+b
Thay x=2 và y=3 vào (d1), ta được:
b+2=3
hay b=1