Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nếu n= 2, tức có hai giá trị x1 và x2, và từ giả thiết ở trên, ta có:
điều phải chứng minh - ở đây \(x_1=a;x_2=b\)
\(\dfrac{a+b}{2}\ge\sqrt{ab}\)
\(\Leftrightarrow a+b\ge2\sqrt{ab}\)
\(\Leftrightarrow a-2\sqrt{ab}+b\ge0\)
\(\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\)
-Dấu đẳng thức trên xảy ra khi: Trung bình cộng lớn hơn hoặc bằng trung bình nhân

Vì a ≥ 0 nên √a xác định, b ≥ 0 nên b xác định
Ta có: a - b 2 ≥ 0 ⇔ a - 2 a b + b ≥ 0
⇒ a + b ≥ 2 a b ⇔ a + b 2 ≥ a b
Dấu đẳng thức xảy ra khi a = b.

Chứng minh bằng biến đổi tương đương :
\(\frac{a+b}{2}\ge\sqrt{ab}\) \(\Leftrightarrow a+b\ge2\sqrt{ab}\Leftrightarrow a+b-2\sqrt{ab}\ge0\Leftrightarrow\left(\sqrt{a}-\sqrt{b}\right)^2\ge\) (luôn đúng)
Bđt cuối luôn đúng nên bđt ban đầu được chứng minh.
Dấu "=" xảy ra khi \(\sqrt{a}-\sqrt{b}=0\Leftrightarrow a=b\) (a,b không âm)

Đặt \(a=x^3,b=y^3,c=z^3\).Áp dụng bất đẳng thức Cô - si với 2 số không âm , ta có
\(\left(x^3+y^3\right)+\left(x^3+xyz\right)\ge2\sqrt{x^3y^3}+2\sqrt{xyz^4}=2\sqrt{xy}\left(xy+z^2\right)\)(1)
\(xy+z^2\ge2\sqrt{xyz^2}=2z\sqrt{xy}\)(2)
Từ (1)(2) \(\Rightarrow x^3+y^3+z^3+xyz\ge2\sqrt{xy}.2z\sqrt{xy}=4xyz\)
\(\Leftrightarrow x^3+y^3+z^3\ge3xyz\)
Vậy \(\frac{a+b+c}{3}\ge\sqrt[3]{abc}\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x=y\\xy=z^2\end{cases}\Leftrightarrow x=y=z\Leftrightarrow a=b=c}\)
P/s tham khảo nha

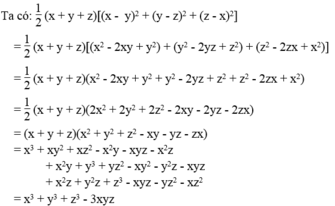
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu a ≥ 0, b ≥ 0, c ≥ 0 thì :
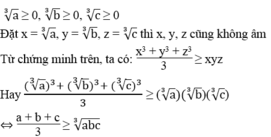

\(\frac{a+b}{2}\ge\sqrt{ab}\Leftrightarrow\frac{a+b}{2}-\sqrt{ab}\ge0\)
\(\Leftrightarrow\frac{a-2\sqrt{ab}+b}{2}\ge0\Leftrightarrow\frac{\left(\sqrt{a}-\sqrt{b}\right)^2}{2}\ge0\)
Dấu ''='' xảy ra khi a = b

Áp dụng bất đẳng thức Cô-si cho hai số không âm, ta có :
\(\dfrac{a+b}{2}\ge\sqrt{ab}\) (1)
\(\dfrac{b+c}{2}\ge\sqrt{bc}\) (2)
\(\dfrac{c+a}{2}\ge\sqrt{ca}\) (3)
Cộng từng vế bất đẳng thức (1), (2), (3) ta được :
\(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Vậy bất đẳng thức đã được chứng minh
Mở rộng cho bốn số a, b, c, d không âm, ta có bất đẳng thức :
\(a+b+c+d\ge\sqrt{ab}+\sqrt{bc}+\sqrt{cd}+\sqrt{da}\)
Mở rộng cho năm số a, b, c, d, e không âm, ta có bất đẳng thức : \(a+b+c+d+e\ge\sqrt{ab}+\sqrt{bc}+\sqrt{cd}+\sqrt{de}+\sqrt{ea}\)
áp dụng BĐT AM-GM với 2 số không âm
\(a+b\ge2\sqrt{ab}\)
\(b+c\ge2\sqrt{bc}\)
\(a+c\ge2\sqrt{ac}\)
cộng các vế của BĐT ta có
\(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)\)
chia cả hai vế của BĐT cho 2 ta có đpcm

1) a2 - ab + b2 ≥ 0
<=> ( 4a2 - 4ab + b2 ) + 3b2 ≥ 0
<=> ( 2a - b )2 + 3b2 ≥ 0 ( đúng ∀ a,b )
Vậy bđt ban đầu được chứng minh
Đẳng thức xảy ra <=> a = b = 0
2) a2 - ab + b2 ≥ 1/4( a + b )2
<=> 4a2 - 4ab + 4b2 ≥ a2 + 2ab + b2
<=> 4a2 - 4ab + 4b - a2 - 2ab - b2 ≥ 0
<=> 3a2 - 6ab + 3b2 ≥ 0
<=> a2 - 2ab + b2 ≥ 0
<=> ( a - b )2 ≥ 0 ( đúng ∀ a,b )
Vậy bđt ban đầu được chứng minh
Đẳng thức xảy ra <=> a = b

áp dụng bất đẳng thức cô- si, ta có:
\(a+b\ge2\sqrt{ab}\) \(\left(1\right)\)
\(b+c\ge2\sqrt{bc}\) \(\left(2\right)\)
\(c+a\ge2\sqrt{ca}\) \(\left(3\right)\)
Cộng (1),(2),(3) vế theo vế, ta được:
\(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\)
\(\Leftrightarrow\) \(a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Dấu " = " xảy ra <=> \(a=b=c\)
![{\displaystyle {\begin{aligned}x_{1}&\neq x_{2}\\[3pt]x_{1}-x_{2}&\neq 0\\[3pt]\left(x_{1}-x_{2}\right)^{2}&\geqslant 0\\[3pt]x_{1}^{2}-2x_{1}x_{2}+x_{2}^{2}&\geqslant 0\\[3pt]x_{1}^{2}+2x_{1}x_{2}+x_{2}^{2}&\geqslant 4x_{1}x_{2}\\[3pt]\left(x_{1}+x_{2}\right)^{2}&\geqslant 4x_{1}x_{2}\\[3pt]{\Bigl (}{\frac {x_{1}+x_{2}}{2}}{\Bigr )}^{2}&\geqslant x_{1}x_{2}\\[3pt]{\frac {x_{1}+x_{2}}{2}}&\geqslant {\sqrt {x_{1}x_{2}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/96dce83e606652266bc8708875bcc82a5b338faa)
áp dụng BĐT cô-si ta có:
\(\frac{a+b}{2}=\frac{a}{2}+\frac{b}{2}\)\(\ge2\sqrt{\frac{a}{2}.\frac{b}{2}}=2\frac{\sqrt{a}\sqrt{b}}{\sqrt{4}}=2\frac{\sqrt{ab}}{2}=\sqrt{ab}\)
Vậy \(\frac{a+b}{2}\ge\sqrt{ab}\)
Dấu đẳng thức xảy ra khi a=b=0 hoặc a=b=1
cái câu hỏi 2 tớ ko bik đúng ko