Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
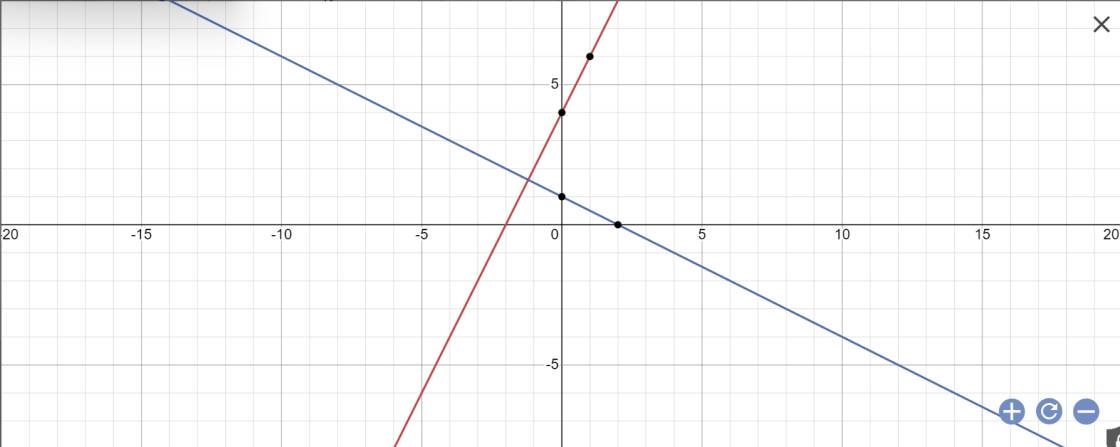
b: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\2x+4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=-4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-2\\y=0\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}x=0\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=2\cdot0+4=4\end{matrix}\right.\)
Tọa độ C là:
\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x+1=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=0\\-\dfrac{1}{2}x=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=0\end{matrix}\right.\)
Tọa độ M là:
\(\left\{{}\begin{matrix}2x+4=-\dfrac{1}{2}x+1\\y=2x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{2}x=-3\\y=2x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-3:\dfrac{5}{2}=-3\cdot\dfrac{2}{5}=-\dfrac{6}{5}\\y=2\cdot\dfrac{-6}{5}+4=\dfrac{-12}{5}+4=\dfrac{8}{5}\end{matrix}\right.\)
A(-2;0); C(2;0); M(-1,2;1,6)
\(AC=\sqrt{\left(2+2\right)^2+\left(0-0\right)^2}=\sqrt{4^2}=4\)
\(AM=\sqrt{\left(-1,2+2\right)^2+\left(1,6-0\right)^2}=\dfrac{4\sqrt{5}}{5}\)
\(CM=\sqrt{\left(-1,2-2\right)^2+1,6^2}=\dfrac{8\sqrt{5}}{5}\)
Vì \(MA^2+MC^2=AC^2\)
nên ΔMAC vuông tại M
c: Vì ΔMAC vuông tại M
nên \(S_{MAC}=\dfrac{1}{2}\cdot MA\cdot MC=\dfrac{1}{2}\cdot\dfrac{4\sqrt{5}}{5}\cdot\dfrac{8\sqrt{5}}{5}=\dfrac{2\cdot8}{5}=\dfrac{16}{5}\)

ai giup vs
Cho x,y là hai số thoả mãn 2(x2+y2)=(x-y)2 Khi đó ta có hệ thức biểu diễn mối quan hệ giữa x,y là x=....y
giải chi tiết nha