
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta chia hình lập phương thành sáu khối tứ diện bằng nhau như sau:
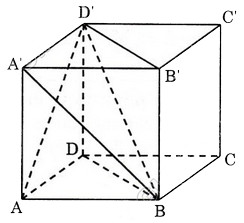
+ Chia khối lập phương ABCD.A’B’C’D’ thành hai khối lăng trụ tam giác bằng nhau: ABD.A’B’D’ và BCD.B’C’D’.
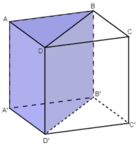
+ Tiếp đó, lần lượt chia khối lăng trụ ABD.A’B’D’ và BCD.B’C’D’ thành ba tứ diện: DABB’, DAA’B’ và DCBB’, DCC’B’, DD’C’B’.
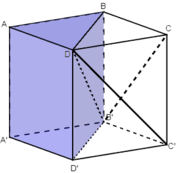
+ Ta chứng minh được các khối tứ diện này bằng nhau như sau:
- Hai khối tứ diện DABB’ và DAA’B’ bằng nhau vì chúng đối xứng nhau qua mặt phẳng (DAB’) (1)
- Hai khối tứ diện DAA’B’ và DD’A’B’ bằng nhau vì chúng đối xứng nhau qua mặt phẳng (B’A’D) (2)
Từ (1) và (2) suy ra ba khối tứ diện DABB’, DAA’B’ và DD’A’B’ bằng nhau.
- Tương tự, ba khối tứ diện DCBB’, DCC’B’, DD’C’B’ cũng bằng nhau.
Vậy khối lập phương ABCD.A’B’C’D’ được chia thành sáu khối tứ diện bằng nhau.

Chọn D
Ta chia khối lập phương thành hai khối lăng trụ đứng;
Ứng với mỗi khối lăng trụ đứng ta có thể chia thành ba khối tứ diện đều mà các đỉnh của tứ diện cũng là đỉnh của hình lập phương.
Vậy có tất cả là 6 khối tứ diện có thể tích bằng nhau.

Chọn B.
Mỗi hình lập phương cạnh a có thể chia thành 8 hình lập phương cạnh bằng a/2, 64 hình lập phương cạnh bằng a/4,... Do đó có thể chia một hình lập phương vô số hình lập phương bằng nhau. Mỗi hình lập phương lại có thể chia thành 6 hình tứ diện bằng nhau. Suy ra, có thể chia một hình lập phương thành vô số hình tứ diện bằng nhau.

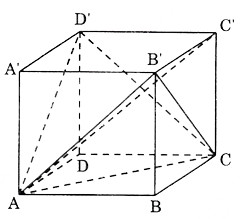
Chia khối lập phương ABCD.A'B'C'D' thành năm khối tứ diện như sau:A'B'CD', A'AB'D', BACB', C'B'CD', DACD'.

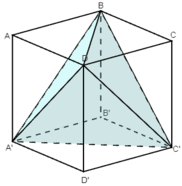
Trong hình bên, ta có thể chia thành năm khối tứ diện là A’ABD; C’CBD; DA’D’C’; BB’A’C’ (4 góc của hình lập phương) và DBA’C’ (tứ diện tô màu).

Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', Phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABA', A'ABD', A'B'BD' bằng nhau
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.
Xem thêm tại: http://loigiaihay.com/bai-4-trang-12-sgk-hinh-hoc-12-c47a4008.html#ixzz4sFfuearg

Cho tứ diện đều ABCD. Gọi G là giao điểm của các đường thẳng nối đỉnh với trọng tâm của mặt đối diện. Khi đó dễ thấy các tứ diện GABC, GBCD, GCDA, GDAB bằng nhau.

Chia khối lập phương ABCD.A′B′C′D′ABCD.A′B′C′D′ thành năm khối tứ diện như sau: AB′CD′,A′AB′D′,BACB′,C′B′CD′,AB′CD′,A′AB′D′,BACB′,C′B′CD′,DACD′
TL ;
Chia khối lập phương ABCD.A'B'C'D' thành năm khối tứ diện như sau:AB'CD', A'AB'D', BACB', C'B'CD', DACD'.
HT

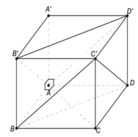
Chia lăng trụ ABD.A'B'D' thành ba tứ diện DABD', A'ABD', A'B'BD'. Phép đối xứng qua (ABD') biến DABD' thành A'ABD', phép đối xứng qua (BA'D') biến A'ABD' thành A'B'BD' nên ba tứ diện DABD', A'ABD', A'B'BD' bằng nhau.
Làm tương tự đối với lăng trụ BCD.B'C'D' ta sẽ chia được hình lập phương thành sáu tứ diện bằng nhau.