
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


b: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x-1}{2}=\dfrac{y-2}{3}=\dfrac{z-3}{4}=\dfrac{2x+3y-z-2-6+3}{2\cdot2+3\cdot3-4}=\dfrac{63}{9}=7\)
Do đó: x=15; y=23; z=31

Có: \(a^2+b+2=2ab\)
\(\Leftrightarrow a^2+2=b\left(2a-1\right)\)
\(\Leftrightarrow b=\frac{a^2+2}{2a-1}\in Z\)
khi và chỉ khi \(a^2+2⋮2a-1\)
\(\Leftrightarrow2\left(a^2+2\right)-a\left(2a-1\right)⋮2a-1\)
\(\Leftrightarrow a+4⋮2a-1\)
\(\Leftrightarrow2\left(a+4\right)-\left(2a-1\right)⋮2a-1\)
\(\Leftrightarrow9⋮2a-1\)
\(\Leftrightarrow2a-1\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Rồi giải a..........
Rồi giải b...........
Bước tiếp theo bn giải nha

\(\left|x^2-3x\right|+\left|\left(x+1\right)\left(x-3\right)\right|=0\)
\(\Leftrightarrow\hept{\begin{cases}\left|x^2-3x\right|=0\\\left|\left(x+1\right)\left(x-3\right)\right|=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x^2-3x=0\\\left(x+1\right)\left(x-3\right)=0\end{cases}}\)
Xét \(x^2-3x=0\)
\(\Rightarrow x\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=3\end{cases}}\)
Xét \(\left(x+1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=3\end{cases}}\)
Vì xét 2 trị biểu thức , một cái có 2 giá trị (0 or 3) , một cái (-1 or 3)
Nên ta lấy cái chung
=> x = 3



ta có: a+b+c=1
<=>(a+b+c)^2=1
<=>ab+bc+ca=0 (1)
mặt khác: áp dụng tính chất dãy tỉ số bằng nhau ta có:
x/a=y/b=z/c=(x+y+z)/(a+b+c)=x+y+z
<=> x=a(x+y+z) ; y=b(x+y+z) ; z=c(x+y+z)
=>xy+yz+zx=ab(x+y+z)^2+bc(x+y+z)^2+ca(x...
<=>xy+yz+zx=(ab+bc+ca)(x+y+z)^2 (2)
từ (1) và (2) ta có đpcm



OK nhưng bn đừng đăng câu hỏi linh tinh nữa nhé
coi chừng bị trừ điểm đấy
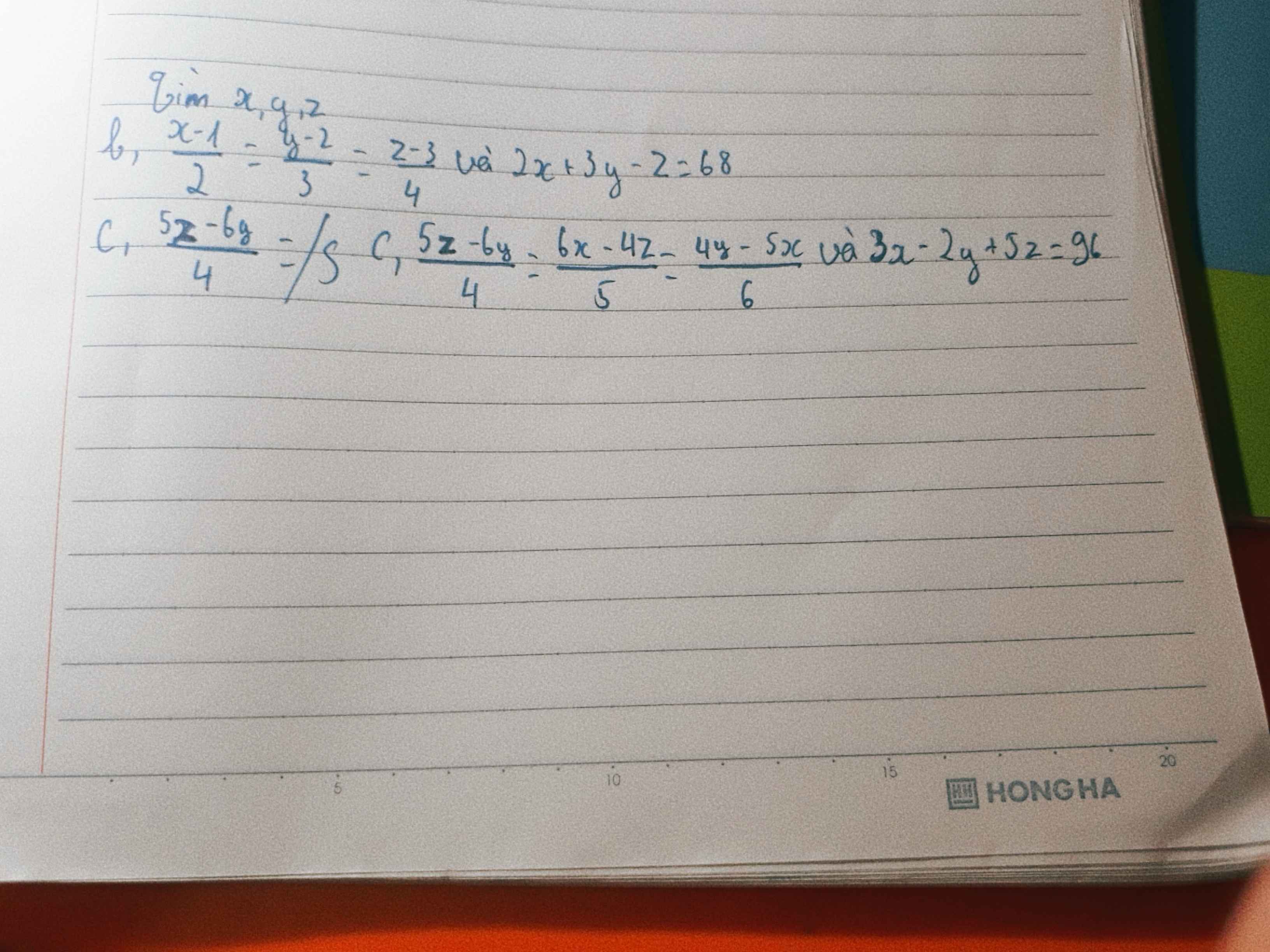
Toàn spam linh tinh thôi
cái gì vậy