Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) 4a72b chia hết cho 2;3;5;9.
Vậy b=0 (chia hết cho 2 và 5 phải có chữ số tận cùng bằng 0).
4a720.
Vậy a=5 (chia hết cho 3 và 9 phải có tổng các chữ số chia hết cho 3 và 9).
45720.
b) a32b chia hết cho 5 và 9
Trường hợp 1:
b=0 (chia hết cho 5 phải có chữ số tận cùng bằng 0 và 5).
a320.
Vậy a=4 (chia hết cho 9 phải có tổng các chữ số chia hết cho 9).
4320.
Trường hợp 2:
b=5 (chia hết cho 5 phải có chữ số tận cùng bằng 0 và 5).
a325.
Vậy a=8 (chia hết cho 9 phải có tổng các chữ số chia hết cho 9).
8325.

A = 1 + 3 + 5 + 7 +... + 990
SSH : (990 - 1 ) : 2 + 1 = 495,5
=> tổng : (1 + 990) . 495,5 : 2 = 245520,25 (để xem số cuối có sai k vậy?)
B = 25 + 83 - 23 * 83
= 25 + 512 - 23 * 512 = -11239
C = 600 : {450 : [450 - (4 * 53 - 23 * 52)]}
= 600 : {450 : [450 - (4 * 125 - 8 * 25)]}
= 600 : {450 : [450 - ( 500 - 200)]
= 600 : {450 : [450 - 300]}
= 600 : {450 : 150}
= 600 : 3 = 200
Bài 2 : a) A chia hết cho 2 => x \(\in\){0;2;4;6;8}
b) A chia hết cho 5 => x \(\in\){0;5 }
c) A chia hết cho 2 và 5 => x = 0
d) A chia hết cho 2 nhưng A ko chia hết cho 5 => x \(\in\){2;4;6;8}
Bài 3 tương tự

Bài 4: Để tìm các chữ số a, b thỏa mãn các điều kiện, ta sẽ kiểm tra từng trường hợp.
a. Để số 4a12b chia hết cho 2, 5 và 9, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 4 + a + 1 + 2 + 0 = 7 + a. Để 7 + a chia hết cho 9, ta có a = 2.
- Nếu b = 5, thì tổng các chữ số là 4 + a + 1 + 2 + 5 = 12 + a. Để 12 + a chia hết cho 9, ta có a = 6.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 6, và b = 0 hoặc b = 5.
b. Để số 5a43b chia hết cho 2, 3 và 5, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 2, nên b phải là số chẵn. Vì số chia hết cho 3, nên tổng các chữ số trong số đó phải chia hết cho 3. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 5 + a + 4 + 3 + 0 = 12 + a. Để 12 + a chia hết cho 3, ta có a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9.
- Nếu b = 5, thì tổng các chữ số là 5 + a + 4 + 3 + 5 = 17 + a. Để 17 + a chia hết cho 3, ta có a = 1 hoặc a = 4 hoặc a = 7.
Vậy, các giá trị thỏa mãn là a = 0 hoặc a = 3 hoặc a = 6 hoặc a = 9, và b = 0 hoặc b = 5.
c. Để số 735a2b chia hết cho 5 và 9, nhưng không chia hết cho 2, ta cần xét chữ số cuối cùng b. Vì số chia hết cho 5, nên b phải là 0 hoặc 5. Vì số chia hết cho 9, nên tổng các chữ số trong số đó phải chia hết cho 9. Ta thử từng trường hợp:
- Nếu b = 0, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 0 = 17 + a. Để 17 + a chia hết cho 9, ta có a = 7 hoặc a = 8.
- Nếu b = 5, thì tổng các chữ số là 7 + 3 + 5 + a + 2 + 5 = 22 + a. Để 22 + a chia hết cho 9, ta có a = 2 hoặc a = 5 hoặc a = 8.
Vậy, các giá trị thỏa mãn là a = 2 hoặc a = 5 hoặc a = 7 hoặc a = 8, và b = 0 hoặc b = 5.
Bài 5: Để xác định xem tổng A có chia hết cho 8 hay không, ta cần tính tổng A và kiểm tra xem nó có chia hết cho 8 hay không.

bài 2:
vì 4a12b chia hết cho cả 2 và 5 nên b=0
để 4a120 chia hết cho 9 thì 4+a+1+2+0 phải chia hết cho 9 => a=2
bài 1:
a/ ta có : 18 = 2x9 => a là số chẵn và 7+3+a chia hết cho 9 => a=8
vậy a=8
b/ để 792a chia hết cho 3 và 5 => a=0 hoặc 5 và 7+9+2+a chia hết cho 3 => a=0
c/ để 87a chia hết cho 5 và 9 => a=0 hoặc a=5 và 8+7+a chia hết cho 9 => ko tìm được a thoả mãn
d/ a=5 và a=8

Ta có thể tìm các bội của một số khác 0 bằng cách nhân số đó lần lược cho 1, 2, 3, …
Ví dụ :
B(5) = {5.1, 4.2, 5.3, …} = {5, 10, 15, …}
Ta có thể tìm các ước của một số a (a > 1) bằng cách lần lược chia số a cho số tự nhiên từ 1 đến a để xét xem a chia hết cho những số nào, khi đó các số ấy là ước của a.

4. x + 16 chia hết cho x + 1
Ta có
x + 16 = ( x + 1 ) + 15
Mà x + 1 chia hết cho 1
=> 15 phải chia hết cho x + 1
=> x + 1 thuộc Ư(15)
Ư(15) = { 1 ; 15 ; 3 ; 5 }
TH1 : x + 1 = 1 => x = 1 - 1 = 0
TH2 : x + 1 = 15 => x = 15 - 1 = 14
TH3 : x + 1 = 3 => x = 3 - 1 = 2
TH4 : x + 1 = 5 => x = 5 - 1 = 4
Vậy x = 0 ; 14 ; 4 ; 2
1
a . Để A chia hết cho 9 thì các số hạng của nó phải chia hết cho 9
Mà 963 , 2439 , 361 chia hết cho 9
=> x cũng phải chia hết cho 9
Vậy điều kiện để A chia hết cho 9 là x chia hết cho 9
Và ngược lại để A ko chia hết cho 9 thì x không chia hết cho 9
b. Tương tự phần trên nha
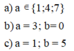
Để \(A=\overline{a32b}\) chia hết cho 5 thì b=0 hoặc b=5
Mà \(A=\overline{a32b}\) không chia hết cho 2 nên b=5
Để \(A=\overline{a325}\) chia hết cho 9 thì (a+3+2+5) chia hết cho 9 hay (a+10) chia hết cho 9
nên a=8
Vậy số A cần tìm là 8325
gg