Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

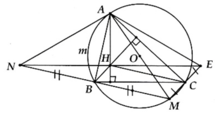
a, BH ^ AC và CM ^ AC Þ BH//CM
Tương tự => CH//BM
=> BHCM là hình bình hành
b, Chứng minh BNHC là hình bình hành
=> NH//BC
=> AH ^ NH => A H M ^ = 90 0
Mà A B N ^ = 90 0 => Tứ giác AHBN nội tiếp
c, Tương tự ý b, ta có: BHEC là hình bình hành. Vậy NH và HE//BC => N, H, E thẳng hàng
d, A B N ^ = 90 0 => AN là đường kính đường tròn ngoại tiếp tứ giác AHBN
AN = AM = 2R, AB = R 3 => A m B ⏜ = 120 0
S A O B = 1 2 S A B M = R 2 3 4
S A m B ⏜ = S a t A O B - S A O B = R 2 12 4 π - 3 3
=> S cần tìm = 2 S A m B ⏜ = R 2 6 4 π - 3 3

1. Gọi giao điểm của CH với AB là I, AH với BC là K,Ta có tứ giác BIHK nội tiếp ⇒I^BK+K^HI=1800màK^HI=A^HC⇒I^BK+A^HC=1800 (1) Ta lại có I^BK=A^MC (hai góc nội tiếp cùng chắn một cung)
A^MC=A^PC (t/c đối xứng) ⇒I^BK=A^PC (2)Từ (1) và (2) ⇒A^PC+A^HC=1800Suy ra tứ giác AHCP nội tiếp.2. Tứ giác AHCP nội tiếp ⇒A^HP=A^CP=A^CMTa lại có A^CM+A^BM=1800⇒A^HP+A^BM=1800 mà A^BM=A^BN
⇒A^HP+A^BN=1800 (3)Chứng minh tương tự câu 1) ta có tứ giác AHBN nội tiếp
⇒A^BN=A^HN (4)
Từ (3) và (4) ⇒A^HP+A^HN=1800⇒ N, H, P thẳng hàng
3. M^AN=2B^AM;M^AP=2M^AC
=> N^AP=2(B^AM+M^AC)=2B^AC (<180độ) không đổi
Có AN = AM = AP, cần chứng minh NP = 2.AP.sinBAC
=> NP lớn nhất <=> AP lớn nhất mà AP = AM
AM lớn nhất <=> AM là đường kính của đường tròn (O)
Vậy NP lớn nhất <=> AM là đường kính của đường tròn.
a)gọi I là giao điểm của CH và AB
K là giao điểm AH và BC
ta có :góc IBK+ AHC=180 độ
mà góc IBK= APC
=> tứ giác AHCP nội tiếp
b)Ta có Góc AHP= ACP cùng chắn cung AP (
mà góc ACP=ACM (1)
=> góc ACP= AHP
cmtt
gócAHN=ABN cùng chắn cung AP
mà ABN=ABM => AHN=ABM(2)
Xét tứ giác ABMC nội tiếp
gócACM+ABM=180 độ (3)
từ (1)(2)(3) =>
góc AHP+AHN=180 độ
=> N,H,P thẳng hàng
ta có góc MAN=2BAM,
góc MAP=2MAC
=> NAP=2(BAM+MAC)
=2 x góc BAC (ko đổi )
ta có AM=AN=AP
NP=2AP.sin BAC=2AM.sinBAC
=> NP lớn nhất <=> AM Max
a) giả sử BHCM là hbh => CH//MB. Mà CH vuông góc với AB... Từ những cái đó => MB vuông góc với AB => góc ABM =90o... theo tính chất góc nội tiếp chắn nửa đường tròn => AM là đường kính