
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn đáp án C.
Gọi M là trung điểm của BC: 
Do tam giác ABC đều nên tâm đường tròn nội tiếp tam giác ABC là trọng tâm, tâm đường tròn ngoại tiếp tam giác ABC
Áp dụng định lí Pytago vào tam giác ABM ta có:



a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước có chia khoảng và compa)
b) Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực (đồng thời là ba đường cao, ba trung tuyến, ba phân giác của tam giác đều ABC).
Ta có: R= OA = AA' =
.
=
.
= √3 (cm).
c) Đường tròn nội tiếp (O;r) tiếp xúc ba cạnh của tam giác đều ABC tại các trung điểm A', B', C' của các cạnh.
r = OA' = AA' =
=
(cm)
d) Vẽ các tiếp tuyến với đường tròn (O;R) tại A,B,C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ∆IJK là tam giác đều ngoại tiếp (O;R).

A B C L' K O J E D I F L
Gọi I là tâm nội tiếp \(\Delta\)ABC, khi đó 3 điểm C,I,K thẳng hàng. Gọi đường tròn ngoại tiếp \(\Delta\)AIE cắt tia CI tại điểm thứ hai F.
Xét \(\Delta\)CKA và \(\Delta\)CIB có: ^ACK = ^BCI (=^ACB/2); ^CAK = ^CBI (=^ABC/2) => \(\Delta\)CKA ~ \(\Delta\)CIB (g.g)
Suy ra: \(\frac{CK}{CI}=\frac{CA}{CB}\). Mà \(\frac{CA}{CB}=\frac{CD}{CA}\)(\(\Delta\)CAD ~ \(\Delta\)CBA) nên \(\frac{CK}{CI}=\frac{CD}{CA}\Rightarrow\frac{CK}{CD}=\frac{CI}{CA}\)
Lại có: CEA và CIF là 2 cát tuyến của (AIE) nên \(\frac{CI}{CA}=\frac{CE}{CF}\). Từ đó: \(\frac{CK}{CD}=\frac{CE}{CF}\)
Suy ra: \(\Delta\)CEK ~ \(\Delta\)CFD (c.g.c) => ^CEK = ^CFD. Nếu ta gọi 2 tia FD và EK cắt nhau ở L' thì ^CEL' = ^CFL'
=> Tứ giác CL'FE nội tiếp => ^ECF = ^EL'F => ^KCD = ^KL'D => Tứ giác CKDL' nội tiếp
Áp dụng phương tích đường tròn có: FK.FC=FD.FL' (1)
Cũng từ \(\Delta\)CKA ~ \(\Delta\)CIB (cmt) => ^BIF = ^AKI hay ^AKF = ^EIC => ^AKF = ^CAF
=> \(\Delta\)AFK ~ \(\Delta\)CFA (g.g) => FA2 = FK.FC (2)
Từ (1) và (2) => FA2 = FD.FL' => \(\Delta\)FDA ~ \(\Delta\)FAL' (c.g.c)
=> ^FL'A = ^FAD = ^DAC - ^FAC = ^ABC - ^FKA = ^ABC - (^KAC + ^ACK) = ^ABC/2 - ^ACB/2
Do đó: ^AL'E = ^FL'A + ^FL'E = ^ABC/2 - ^ACB/2 + ^ACB/2 = ^ABC/2 = ^ABE => Tứ giác ABL'E nội tiếp
Hay tia EK cắt đường tròn ngoại tiếp tam giác ABE tại L' => L' trùng L
Từ đó dễ có: ^BLC = ^ABC/2 + ^ACB + ^ABC/2 + ^BAC/2 = ^ABC + ^ACB + ^BAC/2 = 1800 - ^BAC/2
Vậy thì tâm của đường tròn (BLC) nằm tại điểm chính giữa cung BC chứa A của (O) (đpcm).

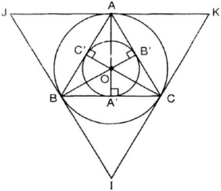
a) Vẽ tam giác đều ABC có cạnh bằng 3cm (dùng thước thẳng và compa).
+ Dựng đoạn thẳng AB = 3cm .
+Dựng cung tròn (A, 3) và cung tròn (B, 3). Hai cung tròn này cắt nhau tại điểm C.
Nối A với C, B với C ta được tam giác đều ABC cạnh 3cm.
b) * Vẽ đường tròn:
Tâm O của đường tròn ngoại tiếp tam giác đều ABC là giao điểm của ba đường trung trực.
Dựng đường trung trực của đoạn thẳng BC và CA.
Hai đường trung trực cắt nhau tại O.
Vẽ đường tròn tâm O, bán kính OA = OB = OC ta được đường tròn ngoại tiếp tam giác ABC.
* Tính bán kính đường tròn.
+ Gọi A’ là trung điểm BC ⇒ A’C = BC/2 = a/2.
và AA’ ⊥ BC
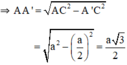
+ Do tam giác ABC là tam giác đều nên 3 đường trung trực đồng thời là ba đường trung tuyến
=> Giao điểm ba đường trung trực cũng là giao điểm ba đường trung tuyến
Suy ra O là trọng tâm tam giác ABC.
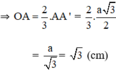
Vậy R = √3 (cm).
c) * Vẽ đường tròn:
Gọi A’; B’; C’ lần lượt là chân đường phân giác trong ứng với các góc 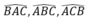
Do tam giác ABC là tam giác đều nên A’; B’; C’ đồng thời là trung điểm BC; CA; AB.
Đường tròn (O; r) là đường tròn tâm O; bán kính OA’ = OB’ = OC’.
* Tính r:
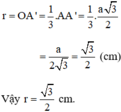
d) Vẽ các tiếp tuyến với đường tròn (O; R) tại A, B, C. Ba tiếp tuyến này cắt nhau tại I, J, K. Ta có ΔIJK là tam giác đều ngoại tiếp (O; R).

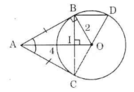
Theo định lí Pitago trong tam giác vuông OAC:
AC2 = OA2 – OC2 = 42 – 22 = 12
=> AC = √12 = 2√3 (cm)
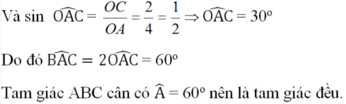
Do đó AB = BC = AC = 2√3 (cm).
Độ dài cạnh tam giác đều là \(a\left(cm\right)\)thì độ dài bán kính đường tròn ngoại tiếp tam giác là \(\frac{a\sqrt{3}}{3}\left(cm\right)\)
\(\frac{a\sqrt{3}}{3}=2\Leftrightarrow a=2\sqrt{3}\left(cm\right)\)