Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\dfrac{AB}{AC}=\dfrac{20}{21}\Rightarrow AB=\dfrac{20AC}{21}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{420^2}=\dfrac{1}{\left(\dfrac{20}{21}AC\right)^2}+\dfrac{1}{AC^2}=\dfrac{841}{400AC^2}\)
\(\Rightarrow AC=609\) \(\Rightarrow AB=\dfrac{20}{21}AC=580\)
\(BC=\sqrt{AB^2+AC^2}=841\)
Chu vị: \(609+580+841=2030\)

Giải:
Ta có: AB:AC = 20 : 21
=> AB:20 = AC:21 (1)
Đặt tỉ số (1) = X,ta có : AB =20X ; AC=21X
Áp dụng định lí PY-TA-GO,ta có:
BC=√(AB2+AC2)=√(20X)2+(21X)2=√(400X2+441X2)=√881X2=29X
Áp dụng hệ thức cạnh và đường cao trong tam giác ABC vuông tại A,ta có:
AH = (ABxAC):BC =(20X x 21X):29X =(140:3) X
=> 420 = (140:3)X => X = 9
=> AB = 20 x 9 = 180 (cm)
=> AC = 21 x 9 = 189 (cm)
=> BC = 29 x 9 =261 (cm)
=> Pabc = 180 + 189 + 261= 630 (cm)

Xét ΔABH và ΔCAH có:
\(\widehat{AHB}=\widehat{CHA}=90\left(gt\right)\)
\(\widehat{ABH}=\widehat{CAH}\) (cùng phụ với \(\widehat{BAH}\) )
=>ΔABH=ΔCAH (g.g)
=>\(\frac{AB}{AC}=\frac{AH}{CH}=\frac{BH}{AH}\)
=>\(\frac{20}{21}=\frac{420}{HC}=\frac{BH}{420}\)
=>\(HC=\frac{420\cdot21}{20}=441\)
\(BH=\frac{420\cdot20}{21}=400\)
=> BC=HC+HB=441+400=841
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(AB^2=BH\cdot BC=400\cdot841=336400\Rightarrow AB=580\)
\(AC^2=HC\cdot BC=441\cdot841=370881\Rightarrow AC=609\)
Vậy chu vi của ΔABC là: AB+AC+BC=580+609+841=2030

Tam giac ABC đồng dạng tam giác HAC (cùng vuông và có chung góc C)
AB/AC = AH/HC = 20/21
HC = 21AH/20 = 441
==> AC = căn(AH^2 + HC^2) =căn(420^2 + 441^2) = 609
AB/AC = 20/21
AB = 20/21*609 = 580
BC = căn(AB^2 + AC^2) = căn(580^2 + 609^2) = 841
Chu vi tam giác ABC = tổng 3 cạnh
C = AB + AC + BC = 580 + 609 + 841 = 2030

Hình vẽ chung cho cả ba bài.
Bài 1:
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}=\frac{1}{15^2}+\frac{1}{20^2}=\frac{1}{144}\)
\(\Rightarrow AH^2=144\Rightarrow AH=12\)
\(BH=\sqrt{AB^2-AH^2}=\sqrt{15^2-12^2}=\sqrt{81}=9\)
\(CH=\sqrt{AC^2-AH^2}=\sqrt{20^2-12^2}=\sqrt{256}=16\)
\(\Rightarrow BC=BH+CH=9+16=25\)
Bài 2,3 bạn nhìn hình vẽ và sử dụng hệ thức lượng để tính tiếp như bài 1.
Bài 2: Bài giải
Đặt BH = x (0 < x < 25) (cm) => CH = 25 - x (cm)
Ta có : \(AH^2=BH\cdot CH\text{ }\Rightarrow\text{ }x\left(25-x\right)=144\text{ }\Rightarrow\text{ }x^2-25x+144=0\)
\(\left(x-9\right)\left(x-16\right)=0\text{ }\Rightarrow\orbr{\begin{cases}x=9\\x=16\end{cases}}\left(tm\right)\)
Nếu BH = 9 cm thì CH = 16 cm \(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
Nếu BH = 16 cm thì CH = 9 cm
\(\Rightarrow\text{ }AB=\sqrt{AH^2+BH^2}=\sqrt{12^2+16^2}=20\text{ }\left(cm\right)\)
\(AC=\sqrt{AH^2+CH^2}=\sqrt{9^2+12^2}=15\text{ }\left(cm\right)\)

a. + CH = 10 - 3.6 = 6.4 (cm)
- Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông vào ΔABC ta có :
+ \(AH^2=BH.CH\)
\(\Rightarrow AH=\sqrt{BH.CH}=\sqrt{3,6.6,4}=4.8\) (cm)
+ \(AB^2=BC.BH\)
\(\Rightarrow AB=\sqrt{BC.BH}=\sqrt{10.3,6}=6\) (cm)
+ \(AC^2=BC.CH\)
\(\Rightarrow AC=\sqrt{BC.CH}=\sqrt{10.6,4}=8\) (cm)
b. \(S_{ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.6.8=24\left(cm^2\right)\)
c. \(P_{ABC}=AB+AC+BC=6+8+10=24\left(cm\right)\)

AB/AC = 20/21 => Đặt AB/20 = AC / 21 = x
=> AB = 20x ; AC= 21x
Tam giác ABC vuông tại A , theo PY TA GO :
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(20x\right)^2+\left(21x\right)^2}=\sqrt{400x^2+441x^2}=\sqrt{881x^2}=29x\)
Tam giác ABC vuông tại A, theo HTL :
AH = \(\frac{AB.AC}{BC}=\frac{20x.21x}{29x}=\frac{140}{3}x\)
=> 420 = 140/3 * x => x = 9
=> AB = 20 . 9 = 180
=> AC = 21.9 = 189
=> BC = 29 . 9 =261
=> Cabc = 180 + 189 + 261= 630

1: AB/AC=5/7
=>HB/HC=(AB/AC)^2=25/49
=>HB/25=HC/49=k
=>HB=25k; HC=49k
ΔABC vuông tại A có AH là đường cao
nên AH^2=HB*HC
=>1225k^2=15^2=225
=>k^2=9/49
=>k=3/7
=>HB=75/7cm; HC=21(cm)
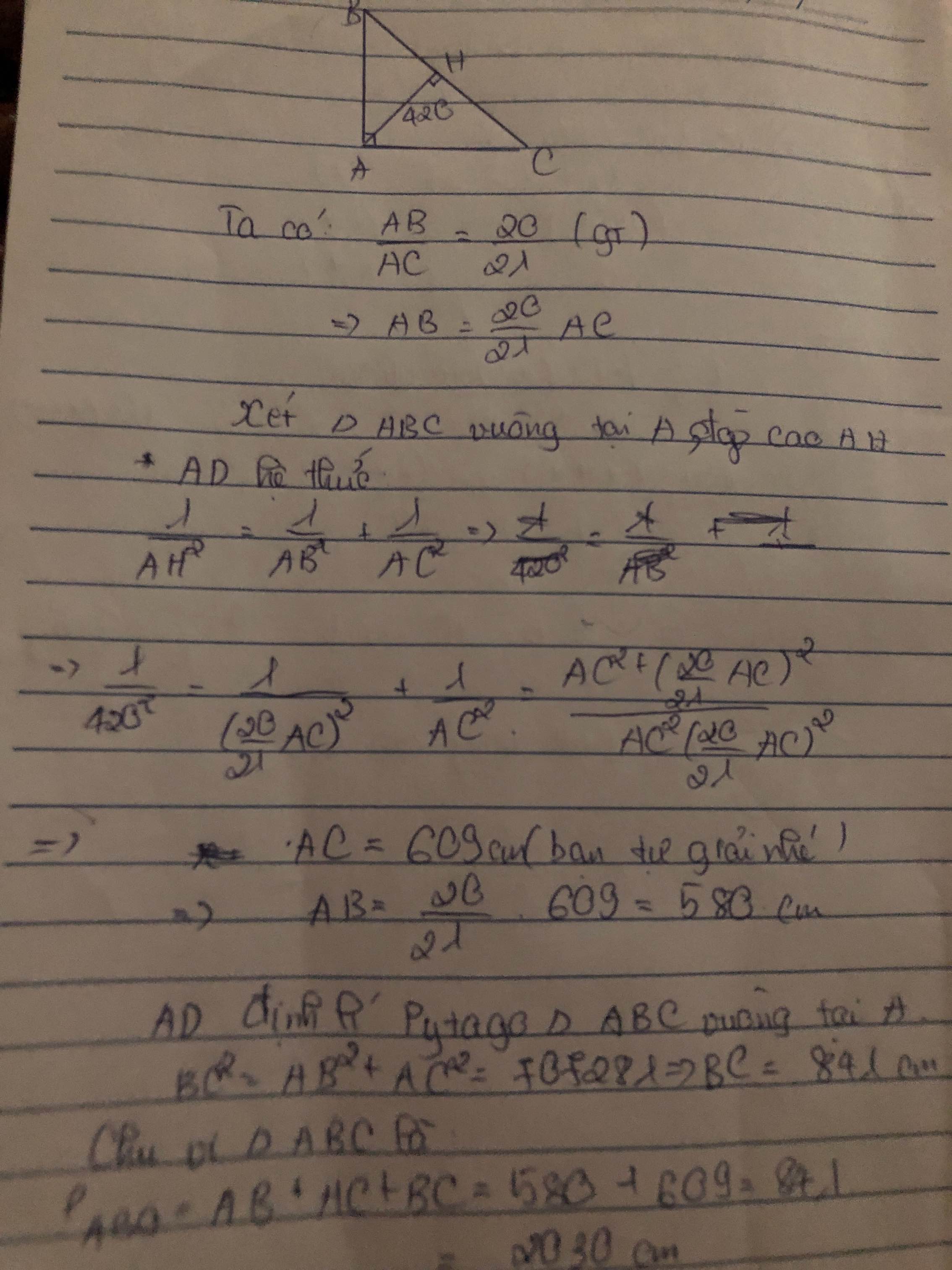

 tham khảo câu tl nàu nhé !
tham khảo câu tl nàu nhé !
Có AB^2 = BC . BH
AC^2 = BC . CH
AB^2 : AC^2 = (BC . BH ) : ( BC . CH)
400/ 441 = BH / CH suy ra BH= 400/ 441 . CH
mà AH2 = BH . CH= CH2 . 400 /441
2402 = CH2 . 400/441
suy ra CH= 252
từ đó tính tiếp nhé