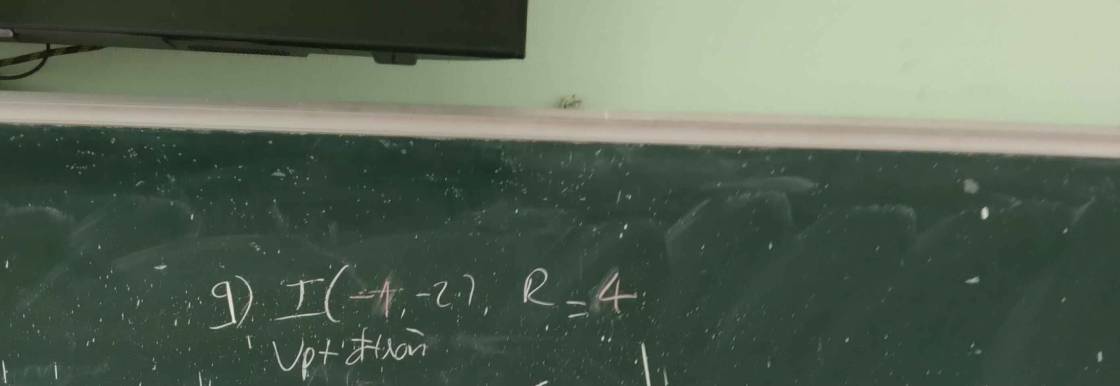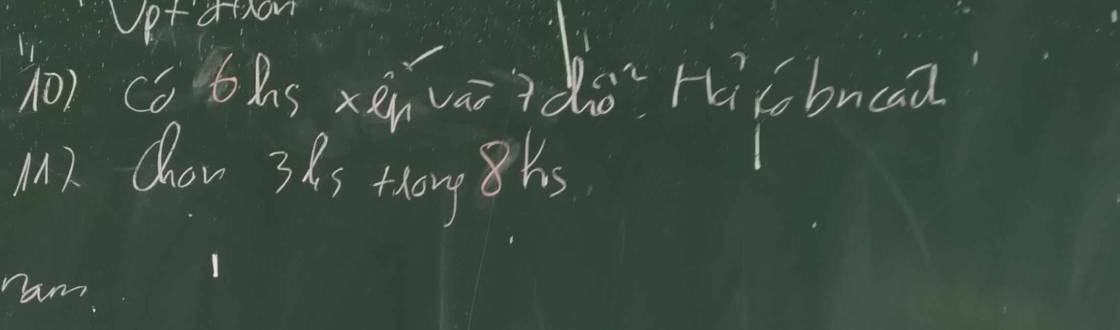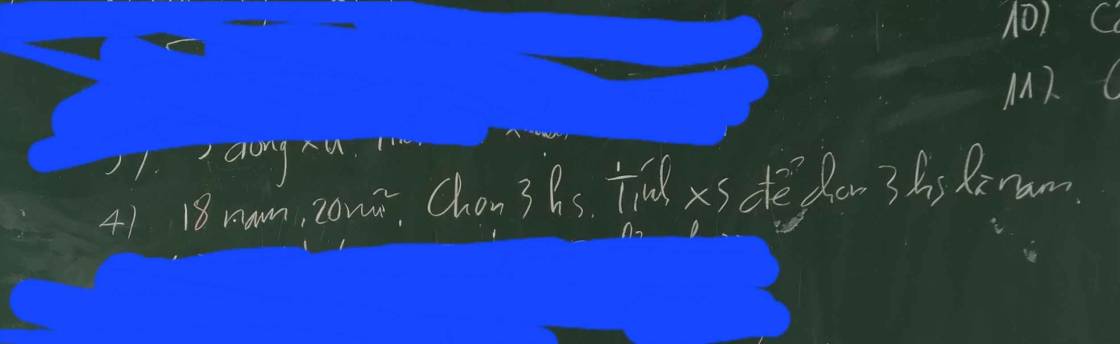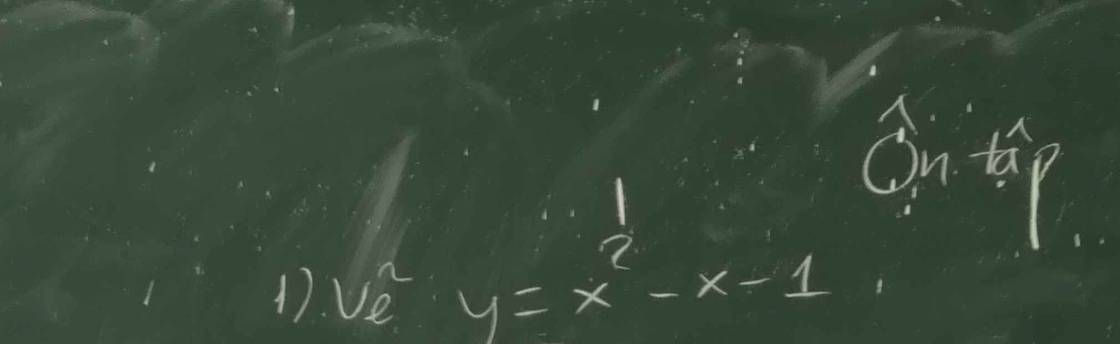K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
DN
1
HP
20 tháng 11 2021
a) (P) có đỉnh I(-1; -2)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{\Delta}{4a}=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2.2\\b^2-4.2.c=8.2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b^2-8c=16\end{matrix}\right.\Leftrightarrow4^2-8c=16\)
\(\Leftrightarrow c=0\)
=> y = 2x2 + 4x
b) (P) có trục đối xứng x = 1 và cắt trục tung tại M(0; 4)
\(M\in\left(P\right)\Rightarrow4=2.0^2+b.0+c\)
\(\Leftrightarrow c=4\)
Trục đối xứng: \(x=-\dfrac{b}{2a}=1\)
<=> -b = 2a
<=> -b = 2.2
<=> b = -4
=> y = 2x2 - 4x + 4
c) Đi qua 2 điểm A(1; 6), B(-1; 0)
\(A\in\left(P\right)\Rightarrow6=2.1^2+b.1+c\)
\(\Leftrightarrow b+c=4\) (1)
\(B\in\left(P\right)\Rightarrow0=2.\left(-1\right)^2+b\left(-1\right)+c\)
\(\Leftrightarrow-b+c=-2\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}b+c=4\\-b+c=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\c=1\end{matrix}\right.\)
=> y = 2x2 + 3x + 1
AT
1
DN
0
DV
1
DV
2
DV
2
2
19 tháng 5 2023
`10)`
Xếp `6` học sinh vào `7` chỗ là `2` lần hoán vị của `6`
`=>` Có `2.6!=1440` cách.
`11)` Chọn `3` học sinh trong `8` học sinh là chỉnh hợp chập `3` của `8`
`=>` Có `A_8 ^3=336` cách.
LD
19 tháng 5 2023
Xếp 6 học sinh vào 7 chỗ là 2 lần hoán vị của 6
⇒ Có 2.6≠1440 cách.
11) Chọn 33 học sinh trong 88 học sinh là chỉnh hợp chập 33 của 88
⇒ Có \(a\dfrac{3}{8}\)=336 cách.
DV
1
DV
2
2
19 tháng 5 2023
`\Omega=C_38 ^3`
Gọi `A:`"Chọn `3` học sinh là nam."
`=>A=C_18 ^3`
`=>P(A)=[C_18 ^3]/[C_38 ^3]=68/703`
LD
19 tháng 5 2023
\(\Omega=c\dfrac{3}{28}\)
gọi a là chọn 3 học sinh là nam
a=\(c\dfrac{3}{18}\)
p(a)=\(\dfrac{c\dfrac{3}{18}}{c\dfrac{3}{38}}\)=\(\dfrac{68}{703}\)
DV
1
