Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

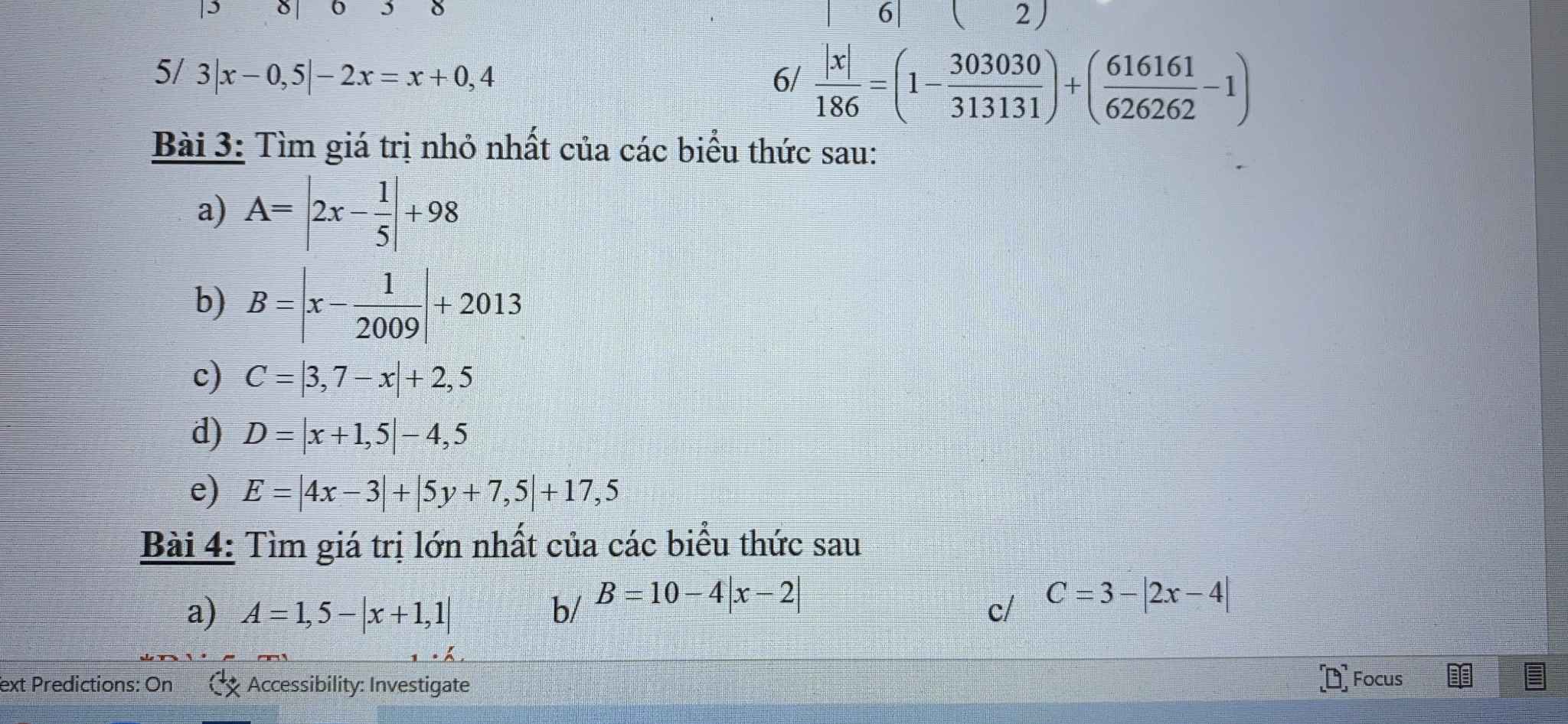
Bài 4:
a: Ta có: \(-\left|x+1.1\right|\le0\forall x\)
\(\Leftrightarrow-\left|x+1.1\right|+1.5\le1.5\forall x\)
Dấu '=' xảy ra khi x=-1,1
b: Ta có: \(-4\left|x-2\right|\le0\forall x\)
\(\Leftrightarrow-4\left|x-2\right|+10\le10\forall x\)
Dấu '=' xảy ra khi x=2

a: AB=6cm
Xét ΔABC có
BA là đường trung tuyến
BM=2/3BA
Do đó:M là trọng tâm của ΔBCD
b: Ta có: M là trọng tâm của ΔBCD
nên DM cắt BC tại trung điểm của BC
hay D,M,E thẳng hàng

Ta có: \(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
mà \(\frac{a}{b}=\frac{c}{d}=\frac{2c}{2d}=\frac{a+2c}{b+2d}\)
\(\Rightarrow\frac{a+c}{b+d}=\frac{a+2c}{b+2d}\)\(\Rightarrow\left(a+c\right)\left(b+2d\right)=\left(b+d\right)\left(a+2c\right)\)( đpcm )

Gọi độ dài 3 cạnh của tam giác là a; b; c (cm) (a;b;c > 0)
Vì các cạnh của tam giác tỉ lệ với 2;4;5 nên ta giả sử
\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}\)
Áp dụng tính chất của dãy tỉ số = nhau ta có:
\(\frac{a}{2}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{2+4+5}=\frac{22}{11}=2\)
\(\Rightarrow\begin{cases}a=2.2=4\\b=2.4=8\\c=2.5=10\end{cases}\)
Vậy độ dài 3 cạnh của tam giác là 4 cm; 8 cm và 10 cm
Gọi các cạnh của tam giác lần lượt là x,y,z (x,y,z>0)
Ta có: \(\frac{x}{2}=\frac{y}{4}=\frac{z}{5}\) và \(x+y+z=22\)
Áp dụng tc của dãy tỉ số bằng nhau ta có:
\(\frac{x}{2}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{2+4+5}=\frac{22}{11}=2\)
=>\(\begin{cases}x=4\\y=8\\z=10\end{cases}\)
Kết luận..........

Gọi đường cao ứng với cạnh \(26cm\) là \(h\left(cm\right)\)
Theo đề bài ta có:
\(26h=35\left(48,8-h\right)\)
\(\Rightarrow26h=1708-35h\)
\(\Rightarrow26h+35h=1708\)
\(\Rightarrow61h=1708\)
\(\Rightarrow h=\frac{1708}{61}\)
\(\Rightarrow h=28\)
Vậy...
S tam giác đều đó lak: 1/2 a. h
\(S=\frac{a\times h}{2}\)
lưu ý: S: diện tích
a: cạnh
h: độ cao
# học tốt #