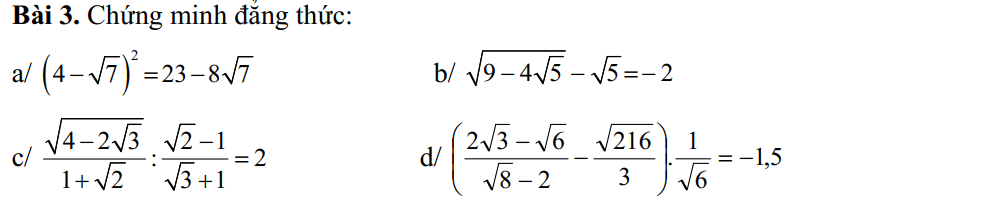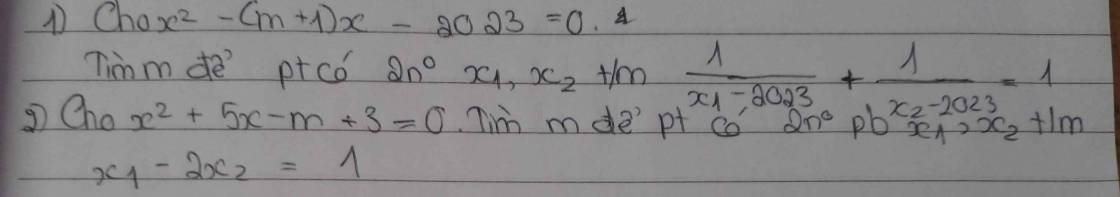K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
21 tháng 8 2020
a. Không giải được\(\sqrt{29}-6\sqrt{6}< 0\)
b. \(\left(\sqrt{8}-3\sqrt{2}-\sqrt{10}\right)\cdot\sqrt{2}-\sqrt{20}\)
=\(\left(2\sqrt{2}-3\sqrt{2}-\sqrt{10}\right)\cdot\sqrt{2}-\sqrt{20}\)
=\(\left(\sqrt{2}-\sqrt{10}\right)\cdot\sqrt{2}-\sqrt{20}\)
21 tháng 8 2020
a) Không thể giải vì \(\sqrt{29}-6\sqrt{6}< 0\)
b) \(\left(\sqrt{8}-3\sqrt{2}-\sqrt{10}\right)\cdot\sqrt{2}-\sqrt{20}\)
=\(\left(2\sqrt{2}-3\sqrt{2}-\sqrt{10}\right)\cdot\sqrt{2}-\sqrt{20}\)
=\(\left(-\sqrt{2}-\sqrt{10}\right)\cdot\sqrt{2}-\sqrt{20}\)
=\(-2-2\sqrt{5}-2\sqrt{5}\)
=\(-2-4\sqrt{5}\)
=\(-2\left(1+2\sqrt{5}\right)\)
25 tháng 6 2016
Gọi số cần tìm là ab điều kiện : a khác 0 ; a , b là chữ số
Theo bài ra , ta có :
a - b = 7 => a = b + 7
ab = ba x 3 + 5 => 10a + b = 30b + 3a + 5 => 7a = 29b + 5 => 7 x ( b + 7 ) 29b + 5 = 7b + 49 = 29b + 5 => 44 = 22b => b = 2
=> a = 7 + 2 = 9
Vậy số cần tìm là : 92
ND
0
ND
0
TM
0
LT
1
12 tháng 1 2024
1: \(x^2-\left(m+1\right)x-2023=0\)
a=1; b=-(m+1); c=-2023
Vì \(a\cdot c=-2023< 0\)
nên phương trình luôn có hai nghiệm phân biệt
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=\dfrac{-\left[-\left(m+1\right)\right]}{1}=m+1\\x_2\cdot x_1=\dfrac{c}{a}=-\dfrac{2023}{1}=-2023\end{matrix}\right.\)
\(\dfrac{1}{x_1-2023}+\dfrac{1}{x_2-2023}=1\)
=>\(\dfrac{x_2-2023+x_1-2023}{\left(x_1-2023\right)\left(x_2-2023\right)}=1\)
=>\(x_2+x_1-4046=\left(x_1-2023\right)\left(x_2-2023\right)\)
=>\(m+1-4046=x_1x_2-2023\left(x_1+x_2\right)+2023^2\)
=>\(m-4045=-2023-2023\left(m+1\right)+2023^2\)
=>\(m-4045=-2023-2023m-2023+2023^2\)
=>\(2024m=4092528\)
=>\(m=\dfrac{4092528}{2024}=2022\)