Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, AB song song với CE(gt) nên góc ABC = góc ECB
AC song song với BE(gt) nên góc ACB = góc EBC
Tam giác ABC = Tam giác ECB (g.c.g) nên AC=BE (2 cạnh tương ứng)
Mà AC =BD (gt) do đó: BD =BE
Vậy tam giác BDE cân tại B
b, Tam giác BDE cân tại B (cmt) suy ra: góc BDC =góc E (t/c)
AC song song với BE(gt) nên góc ACD = góc E (đồng vị)
Tam giác ACD = tam giác BDC (c.g.c)
c, 2 tam giác bằng nhau trên suy ra: góc ADC = góc BCD
Vậy ABCD là hình thang cân (định nghĩa)

a: Xét ΔACB và ΔEBC có
\(\widehat{ABC}=\widehat{ECB}\)(AB//EC)
BC chung
\(\widehat{ACB}=\widehat{EBC}\)(AC//BE)
Do đó: ΔACB=ΔEBC
b: ΔACB=ΔEBC
=>AC=BE
mà AC=BD
nên BE=BD
=>ΔBDE cân tại B
c: ΔBDE cân tại B
=>\(\widehat{BDE}=\widehat{BED}\)
=>\(\widehat{BDC}=\widehat{BED}\)
mà \(\widehat{BED}=\widehat{ACD}\)(AC//BE)
nên \(\widehat{ACD}=\widehat{BDC}\)

a/vì AB//DC(gt) suy ra AB//DE
và AC//BE(gt)
do hai đoạn thẳng song song(AB//DE) chắn bởi 2 đường thẳng song song (AC//BE) suy ra AC=BE
Mà AC=BD(gt)
suy ra BD=BE
Trong tam giác BDE có BD=BE suy ra tam giác BDE cân tại B (dpcm)
b/Chứng minh:tg ACD=tg BDC
VÌ tg BDE cân tại B nên ta có :GÓc B1 = GÓc E1(*)
Vì AC//BE(gt)
E=C1 là 2 góc đồng vị
suy ra góc C1 =góc E(**)
từ (*);(**) suy ra B1=C1
bạn tự xét tg nha
suy ra tg ACD=tg BDC
c/bạn tự cm lun nha

a, Ta có: BE song song AC ( theo bài ra)
AB song song CE ( E thuộc CD)
nên ABEC là hình bình hành, do đó AC=BE
mà AC = BD
nên BD=BE do đó BDE là tam giác cân
b, Ta có AC song song BE nên ˆBEC=ˆACD
mà ˆBED=ˆBDC ( BDE là tam giác cân )
do đó ˆACD=ˆBDC
Xét tg ACD và tg BDC có : ˆACD=ˆBDC
AC=BD( theo gt )
BC là cạnh chung
nên tg ACD =tg BDC ( c-g-c)
c, Theo chứng minh câu b, ta có: tg ACD= tg BDC
do đó ˆADC=ˆBCD
Vậy ABCD là hình thang cân

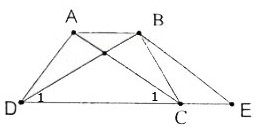
A B E C D 1 1
a) Hình thang ABEC ( AB // CE ) có hai cạnh bên AC, BE song song nên chúng bằng nhau: AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó \(\Delta BDE\)cân
b) Do AC // BE nên \(\widehat{E}=\widehat{C_1}\left(3\right)\)
Mà tam giác BDE cân tại B ( câu a ) nên \(\widehat{E}=\widehat{D_1}\left(4\right)\)
Từ (3)(4) => \(\widehat{D_1}=\widehat{C_1}\)
* Xét 2 tam giác : ACD và BDC có :
DC chung
AC = BD ( gt )
\(\widehat{C_1}=\widehat{D_1}\left(cmt\right)\)
\(\Rightarrow\Delta ACD=\Delta BDC\left(c-g-c\right)\)
c) Theo ( c/m câu b ) ta có :
\(\Delta ACD=\Delta BDC\)
nên \(\widehat{ADC}=\widehat{BCD}\)( 2 góc tương ứng )
Vậy hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.

bạn tự vẽ hình nhé :)
a) ABCE là hình thang có 2 cạnh bên song song => AC=BE mà AC=BD => BE=BD => tam giác BDE cân tại B
b) tam giác BDE cân tại B => góc BDC=góc E mà góc ACD=góc E (2 góc đồng vị, AC//BE) => góc BDC= góc ACD
từ đó, chứng minh đc tg ACD=BDC (c-g-c)
c) tg ACD=BDC => góc ADC=góc BCD (2 góc tương ứng) => đpcm
tg BDE cân tại B:
ta có:ACD=BAC(AB//CD)
mà ACD =BEC =>BEC=BAC
xét tg ABC va tg ECB
+BC chung
+ACB=EBC(so le trong)
+BEC=BAC(cm trên )
=>tam giac ABC =tam giac ECB
=>BDC=BEC
ma `BEC=ACD(đồng vị)
=>ACD=BDC
xét tg ACD va tg BDC,ta có :
+DC chung
+ACD=BDC
+AC=BD(gt)
=>tg ACD = tg BDC
=>ADC=BCD
=>ABCD la hình thang cân (đpcm)

a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:
AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 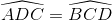
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
Bài giải:
a) Hình thang ABEC (AB // CE) có hai cạnh bên AC, BE song song nên chúng bằng nhau:

AC = BE (1)
Theo giả thiết AC = BD (2)
Từ (1) và (2) suy ra BE = BD do đó tam giác BDE cân.
b) Ta có AC // BE suy ra  =
=  (3)
(3)
∆BDE cân tại B (câu a) nên  =
=  (4)
(4)
Từ (3) và (4) suy ra  =
= 
Xét ∆ACD và ∆BCD có AC = BD (gt)
 =
=  (cmt)
(cmt)
CD cạnh chung
Nên ∆ACD = ∆BDC (c.g.c)
c) ∆ACD = ∆BDC (câu b)
Suy ra 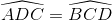
Hình thang ABCD có hai góc kề một đáy bằng nhau nên là hình thang cân.
câu b là đúng
Các bạn giải hộ mình vs