
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 1:
Vận tốc cano khi dòng nước lặng là: $25-2=23$ (km/h)
Bài 2:
Đổi 1 giờ 48 phút = 1,8 giờ
Độ dài quãng đường AB: $1,8\times 25=45$ (km)
Vận tốc ngược dòng là: $25-2,5-2,5=20$ (km/h)
Cano ngược dòng từ B về A hết:
$45:20=2,25$ giờ = 2 giờ 15 phút.

Bài 1:
a.
$a^3-a^2c+a^2b-abc=a^2(a-c)+ab(a-c)$
$=(a-c)(a^2+ab)=(a-c)a(a+b)=a(a-c)(a+b)$
b.
$(x^2+1)^2-4x^2=(x^2+1)^2-(2x)^2=(x^2+1-2x)(x^2+1+2x)$
$=(x-1)^2(x+1)^2$
c.
$x^2-10x-9y^2+25=(x^2-10x+25)-9y^2$
$=(x-5)^2-(3y)^2=(x-5-3y)(x-5+3y)$
d.
$4x^2-36x+56=4(x^2-9x+14)=4(x^2-2x-7x+14)$
$=4[x(x-2)-7(x-2)]=4(x-2)(x-7)$
Bài 2:
a. $(3x+4)^2-(3x-1)(3x+1)=49$
$\Leftrightarrow (3x+4)^2-[(3x)^2-1]=49$
$\Leftrightarrow (3x+4)^2-(3x)^2=48$
$\Leftrightarrow (3x+4-3x)(3x+4+3x)=48$
$\Leftrightarrow 4(6x+4)=48$
$\Leftrightarrow 6x+4=12$
$\Leftrightarrow 6x=8$
$\Leftrightarrow x=\frac{4}{3}$
b. $x^2-4x+4=9(x-2)$
$\Leftrightarrow (x-2)^2=9(x-2)$
$\Leftrightarrow (x-2)(x-2-9)=0$
$\Leftrightarrow (x-2)(x-11)=0$
$\Leftrightarrow x-2=0$ hoặc $x-11=0$
$\Leftrightarrow x=2$ hoặc $x=11$
c.
$x^2-25=3x-15$
$\Leftrightarrow (x-5)(x+5)=3(x-5)$
$\Leftrightarrow (x-5)(x+5-3)=0$
$\Leftrightarrow (x-5)(x+2)=0$
$\Leftrightarrow x-5=0$ hoặc $x+2=0$
$\Leftrightarrow x=5$ hoặc $x=-2$

a) \(\sqrt{169}=13\) và \(\sqrt{196}=14\)
bài 3 :
a) \(A=\frac{\sqrt{72}}{\sqrt{2}}+2\frac{\sqrt{27}}{\sqrt{3}}-3\frac{\sqrt{28}}{\sqrt{63}}=\frac{22}{3}\)tương tự

Bài 2:
a: \(\Leftrightarrow4x^2=9\)
=>(2x-3)(2x+3)=0
hay \(x\in\left\{\dfrac{3}{2};-\dfrac{3}{2}\right\}\)
b: \(\Leftrightarrow4x^2-4x+1-4x^2+12x-x+3=-3\)
\(\Leftrightarrow7x+4=-3\)
hay x=-1
Bài 3:
x=2013
nên x+1=2014
\(A=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+2014\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+2014\)
=2014-x
=2014-2013=1


b) Bạn đã chứng minh được tứ giác EKFC là hình bình hành ở câu a, mà EF cắt CK tại I \(\Rightarrow\)I là trung điểm EF (tính chất hình bình hành)
\(\Rightarrow AI\)là trung tuyến của \(\Delta AEF\)
Mà \(\Delta AEF\)vuông tại A \(\Rightarrow AI=\frac{1}{2}EF\)(tính chất tam giác vuông)
Lại có \(EI=\frac{1}{2}EF\)do I là trung điểm của đoạn EF \(\Rightarrow AI=EI\left(=\frac{1}{2}EF\right)\)
Mặt khác \(BE\perp AF\), \(MI\perp AF\left(gt\right)\)\(\Rightarrow BE//MI\)(quan hệ từ vuông góc đến song song)
Mà tứ giác BEFD là hình bình hành \(\Rightarrow BD//EF\)(tính chất hình bình hành)
\(\Rightarrow BM//EI\)(vì \(M\in BD;I\in EF\))
Xét tứ giác BEIM có \(BE//MI\left(cmt\right);BM//EI\left(cmt\right)\)\(\Rightarrow\)Tứ giác BEIM là hình bình hành (định nghĩa)
\(\Rightarrow BM=EI\)(tính chất hình bình hành)
Mà \(AI=EI\left(cmt\right)\)\(\Rightarrow AI=BM\left(=EI\right)\left(đpcm\right)\)
c) Do tứ giác BEFD là hình bình hành \(\Rightarrow\hept{\begin{cases}BE//DF\\BE=DF\end{cases}}\)(tính chất hình bình hành)
Mà \(\hept{\begin{cases}BE\perp CF\\BE=CF\end{cases}}\left(gt\right)\Rightarrow\hept{\begin{cases}DF\perp CFtạiF\\DF=CF\end{cases}}\)\(\Rightarrow\)F nằm trên đường trung trực của đoạn CD và \(\Delta CDF\)vuông cân tại F
\(\Rightarrow\widehat{DCF}=45^0\)
\(\Delta ABC\)vuông cân tại A (gt) \(\Rightarrow\widehat{ACB}=45^0\)
\(\Rightarrow\widehat{BCD}=180^0-\widehat{ACB}-\widehat{DCF}=180^0-45^0-45^0=90^0\)
\(\Rightarrow\Delta BCD\)vuông tại C.
Xét hình thang BEFD (BE//DF) ta có I là trung điểm EF (cmt) và IM//BE (cmt) \(\Rightarrow\)M là trung điểm của đoạn BD
\(\Rightarrow\)CM là trung tuyến của \(\Delta BCD\)
Mặt khác \(\Delta BCD\)vuông tại C \(\Rightarrow CM=\frac{1}{2}BD\)(tính chát tam giác vuông)
Mà \(DM=\frac{1}{2}BD\)do M là trung điểm BD \(\Rightarrow DM=CM\left(=\frac{1}{2}BD\right)\)
\(\Rightarrow\)M nằm trên đường trung trực của đoạn CD.
Mà F cũng nằm trên đường trung trực của đoạn CD (cmt)
\(\Rightarrow\)MF là đường trung trực của đoạn CD \(\Rightarrow\)C đối xứng với D qua MF (đpcm)

Trong sách có mà bạn ( Ít nhất cũng thuộc chứ )
1. Bình phương của một tổng:
\(\left(a+b\right)^2=a^2+2ab+b^2\)
2. Bình phương của một hiệu:
\(\left(a-b\right)^2=a^2-2ab+b^2\)
3. Hiệu hai bình phương:
\(a^2-b^2=\left(a-b\right)\left(a+b\right)\)
4. Lập phương của một tổng:
\(\left(a+b\right)^3=a^3+3a^2b+3ab^2+b^3\)
5. Lập phương của một hiệu:
\(\left(a-b\right)^3=a^3-3a^2b+3ab^2-b^3\)
6. Tổng hai lập phương:
\(a^3+b^3=\left(a+b\right)\left(a^2-ab+b^2\right)=\left(a+b\right)^3-3a^2b-3ab^2=\left(a+b\right)^3-3ab\left(a+b\right)\)
7. Hiệu hai lập phương:
\(a^3-b^3=\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)^3+3a^2b-3ab^2=\left(a-b\right)^3+3ab\left(a-b\right)\)
Hok tốt

Bài giải:
a) (x2 – 2x+ 1)(x – 1)
= x2 . x + x2.(-1) + (-2x). x + (-2x). (-1) + 1 . x + 1 . (-1)
= x3 - x2 - 2x2 + 2x + x – 1
= x3 - 3x2 + 3x – 1
b) (x3 – 2x2 + x -1)(5 – x)
= x3 . 5 + x3 . (-x) + (-2 x2) . 5 + (-2x2)(-x) + x . 5 + x(-x) + (-1) . 5 + (-1) . (-x)
= 5 x3 – x4 – 10x2 + 2x3 +5x – x2 – 5 + x
= - x4 + 7x3 – 11x2+ 6x - 5.
Suy ra kết quả của phép nhan:
(x3 – 2x2 + x -1)(x - 5) = (x3 – 2x2 + x -1)(-(5 - x))
= - (x3 – 2x2 + x -1)(5 – x)
= - (- x4 + 7x3 – 11x2+ 6x -5)
= x4 - 7x3 + 11x2- 6x + 5
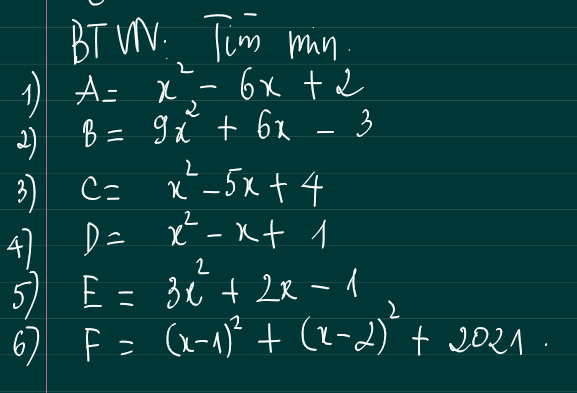


 Các bạn giúp mình giải bài này đi mình xin cảm ơn
Các bạn giúp mình giải bài này đi mình xin cảm ơn


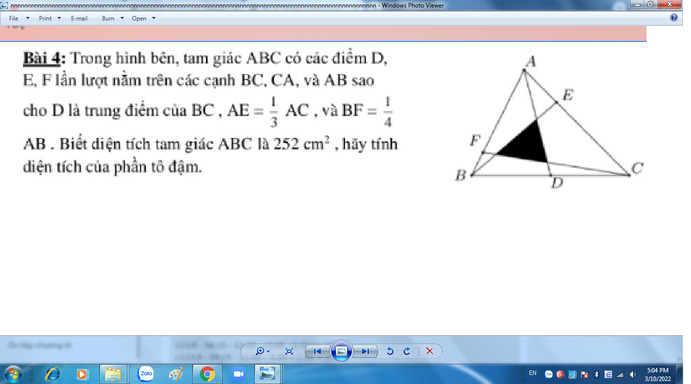
 GIÚP MÌNH BÀI 4 CÂU B,C THÔI Ạ MÌNH CẢM ƠN NHIỀU
GIÚP MÌNH BÀI 4 CÂU B,C THÔI Ạ MÌNH CẢM ƠN NHIỀU
4: \(D=x^2-2\cdot x\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{1}{2}\)
\(A=\left(x^2-6x+9\right)-7=\left(x-3\right)^2-7\ge7\\ A_{min}=7\Leftrightarrow x=3\\ B=\left(9x^2+6x+1\right)-4=\left(3x+1\right)^2-4\ge-4\\ B_{min}=-4\Leftrightarrow x=-\dfrac{1}{3}\\ C=\left(x^2-2\cdot\dfrac{5}{2}x+\dfrac{25}{4}\right)-\dfrac{9}{4}=\left(x-\dfrac{5}{2}\right)^2-\dfrac{9}{4}\ge-\dfrac{9}{4}\\ C_{min}=-\dfrac{9}{4}\Leftrightarrow x=\dfrac{5}{2}\\ D=\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{3}{4}=\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\\ D_{min}=\dfrac{3}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(E=3\left(x^2+2\cdot\dfrac{1}{3}x+\dfrac{1}{9}\right)-\dfrac{4}{3}=3\left(x+\dfrac{1}{3}\right)^2-\dfrac{4}{3}\ge-\dfrac{4}{3}\\ E_{min}=-\dfrac{4}{3}\Leftrightarrow x=-\dfrac{1}{3}\\ F=x^2-2x+1+x^2-4x+4+2021\\ F=2\left(x^2-3x+\dfrac{9}{4}\right)+\dfrac{4031}{2}=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{4031}{2}\ge\dfrac{4031}{2}\\ F_{min}=\dfrac{4031}{2}\Leftrightarrow x=\dfrac{3}{2}\)