K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
và B = 
![\displaystyle a=\sqrt[3]{{2-\sqrt{3}}}+\sqrt[3]{{2+\sqrt{3}}}](https://toancap2.net/wp-content/ql-cache/quicklatex.com-f97fff04475ef931060f897e441e2052_l3.svg)
. Chứng minh 
là số nguyên
25 tháng 2 2020
????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????????/
TL
3
8 tháng 10 2017
\(A=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}=\left|x+1\right|+\left|x-1\right|\)
\(=\left|x+1\right|+\left|1-x\right|\ge\left|x+1+1-x\right|\)\(\ge2\)
Dấu "=" xảy ra khi và chỉ khi \(\hept{\begin{cases}x+1\ge0\\x-1\le0\end{cases}\Rightarrow\hept{\begin{cases}x\ge-1\\x\le1\end{cases}}}\)
vậy Amin= 2 \(\Leftrightarrow-1\le x\le1\)
8 tháng 10 2017
\(A=\sqrt{x^2+2x+1}+\sqrt{x^2-2x+1}=\sqrt{\left(x+1\right)^2}+\sqrt{\left(x-1\right)^2}\)
\(=\left|x+1\right|+\left|x-1\right|=\left|x+1\right|+\left|1-x\right|\ge\left|x+1+1-x\right|=2\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x+1\right)\left(1-x\right)\ge0\Leftrightarrow-1\le x\le1\)
Vậy \(A_{min}=2\) tại \(-1\le x\le1\)
DH
= ....................
1
26 tháng 11 2017
TA CÓ :\(5+2\sqrt{6}=\left(\sqrt{3}+\sqrt{2}\right)^2\)
\(\Rightarrow\frac{\sqrt{5+2\sqrt{6}}}{\sqrt{3}+\sqrt{2}}+2014=\frac{\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}}{\sqrt{3}+\sqrt{2}}+2014\)
\(=1+2014=2015\)
Vậy giá trị biểu thức là 2015.
UK
10 tháng 11 2017
a) Từ gt, suy ra
\(\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x^2-xy+y^2\right)+\left(x^2+2xy+y^2\right)+4\left(x+y\right)+4=0\)
\(\Leftrightarrow\left(x^2-xy+y^2\right)\left(x+y+2\right)+\left(x+y+2\right)^2=0\)
\(\Leftrightarrow\dfrac{1}{2}\left(x+y+2\right)\left(2x^2-2xy+2y^2+2x+2y+4\right)=0\)
\(\Leftrightarrow\dfrac{1}{2}\left(x+y+2\right)\left[\left(x-y\right)^2+\left(x+1\right)^2+\left(y+1\right)^2+2\right]=0\)
Do đó: \(x+y+2=0\Leftrightarrow x+y=-2\)
Mặt khác \(xy>0\Rightarrow x< 0;y< 0\)
Áp dụng AM-GM, ta có
\(\sqrt{\left(-x\right)\left(-y\right)}\le\dfrac{\left(-x\right)+\left(-y\right)}{2}=1\) nên \(xy\le1\)\(\Rightarrow\dfrac{-2}{xy}\le-2\)
\(M=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{x+y}{xy}\le-2\)
GTLN của M là -2 khi x=y=-1
UK
10 tháng 11 2017
Áp dụng Cauchy-Schwarz dạng Engel, ta có
\(VT=\dfrac{a^6}{a^3+a^2b+b^2a}+\dfrac{b^6}{b^3+b^2c+c^2b}+\dfrac{c^6}{c^3+c^2a+ca^2}\ge\dfrac{\left(a^3+b^3+c^3\right)^2}{a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)}\)
Mặt khác: \(\left(a-b\right)^2\ge0\Leftrightarrow a^2-ab+b^2\ge ab\Leftrightarrow a^3+b^3\ge ab\left(a+b\right)\)
Tương tự: \(b^3+c^3\ge bc\left(b+c\right);c^3+a^3\ge ca\left(c+a\right)\)
\(\Rightarrow2\left(a^3+b^3+c^3\right)\ge ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\)
\(3\left(a^3+b^3+c^3\right)\ge a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)\)
\(\Rightarrow\dfrac{\left(a^3+b^3+c^3\right)^2}{a^3+b^3+c^3+ab\left(a+b\right)+bc\left(b+c\right)+ca\left(c+a\right)}\ge\dfrac{a^3+b^3+c^3}{3}\)
Vậy ta có đpcm. Đẳng thức xảy ra khi và chỉ khi a=b=c
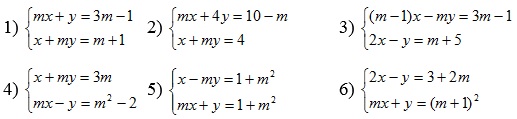