Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


VE HINH
â) Xét tứ giác KCID ,co:
gocI = (cungAB+cungCD):2 = (180+60):2 = 120 độ
gocK=(cungAB-cungCD):2 =(180-60):2=60 độ
gócI+gocK=120do+60do=180 do
Vay : tứ giác KCID nội tiếp (tổng số đo 2 góc đối diện=180 độ )
:góc AKB = 60 độ
b)Ta có:AB//CD
=>cungAC=cungBD=(180-60):2=60 do (2 cung nằm giữa 2 dây song song thì = nhau )
=>AC=BD(2 dây chan 2 cung = nhau thi = nhau ) (1)
=>tứ giác ACDB là hình thang cân
***Xét : 3giac AKDva 3giac BKC ,co:
gocD=gocC=90do (vi gocC va gocD là góc nội tiếp chắn nửa đường tròn)
gocCAD=gocDBC(2goc noi tiep cung chan cungCD)
AD=BC(2 đường chéo của hình thang cân thì = nhau )(cmt)
Do do:3giacAKD =3giacBKC (g-c-g)
=>KD=KC (2 canh tương ứng) (2)
Ta lại có :KA=KC+AC(C nam giua A va K)
}(3)
:KB=KD+BD(D nam giua B va K)
Tu (1) ,(2) va (3) suy ra KA=KB (4)
Tu (2) va (4) suy ra KA.KC=KB.KD .

a: Xét (O) có
ΔBAC nội tiếp
AC là đường kính
Do đó: ΔBAC vuông tại B
Xét (O) có
\(\widehat{BAC}\) là góc nội tiếp chắn cung BC
Do đó: \(\widehat{BAC}=\dfrac{1}{2}\cdot sđ\stackrel\frown{BC}=\dfrac{1}{2}\cdot60^0=30^0\)
Gọi H là giao điểm của BD với AC
BD\(\perp\)AC nên BD\(\perp\)AC tại H
ΔOBD cân tại O
mà OH là đường cao
nên H là trung điểm của BD
Xét ΔCBD có
CH là đường cao
CH là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD
Xét ΔCOD và ΔCOB có
CD=CB
OD=OB
CO chung
Do đó: ΔCOD=ΔCOB
=>\(\widehat{COD}=\widehat{COB}\)
=>\(sđ\stackrel\frown{CB}=sđ\stackrel\frown{CD}=60^0\)
Xét ΔBAC vuông tại B có \(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(\widehat{BCA}+30^0=90^0\)
=>\(\widehat{BCA}=60^0\)
Xét (O) có
\(\widehat{BCA}\) là góc nội tiếp chắn cung AB
Do đó: \(\widehat{BCA}=\dfrac{1}{2}\cdot sđ\stackrel\frown{AB}\)
=>\(sđ\stackrel\frown{AB}=2\cdot\widehat{BCA}=120^0\)
DF//AC
DB\(\perp\)AC
Do đó: DF\(\perp\)DB
=>ΔDFB vuông tại D
ΔDFB vuông tại D
nên ΔDFB nội tiếp đường tròn đường kính BF
mà ΔDFB nội tiếp (O)
nên O là trung điểm của BF
=>OA//DF
=>\(\widehat{BFD}=\widehat{BOH}=\widehat{BOC}\)(hai góc đồng vị)
=>\(\widehat{BFD}=60^0\)
ΔBDF vuông tại D
=>\(\widehat{BFD}+\widehat{FBD}=90^0\)
=>\(\widehat{FBD}+60^0=90^0\)
=>\(\widehat{FBD}=30^0\)
Xét (O) có
\(\widehat{FBD}\) là góc nội tiếp chắn cung FD
Do đó: \(\widehat{FBD}=\dfrac{1}{2}\cdot sđ\stackrel\frown{FD}\)
=>\(sđ\stackrel\frown{FD}=2\cdot\widehat{FBD}=2\cdot\)30=60 độ

Có thể giải gúp tôi được không /
Con mua 17 kg cam , mẹ mua gấp 3 lần số cam của con . Hỏi cả hai mẹ con mua được bao nhiêu kg cam ?

a) vuông, nên
Kc là tiếp tuyến, KEF là cát tuyến nên
Suy ra , nên
Ta có nên , từ đó EMOF là tứ giác nội tiếp. (1)
b) Đặt . Ta có ... )uôn nên là ến, KFàcáê u êT c\(DeltaKM\simDetaF.g êtđó O àt gánội ế 1)ặ aó ,nên là tứ iá ộ tip. (2ừ (1) ()y ramđi A , F tộc cng một đường đườgính ủ

a) Trong tứ giác AOBM có 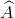 =
= 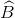 =
= 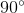 .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 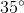
= 
b) Từ 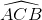 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 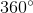 -
-  =
=