Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Bảng 6:
| Lớp nhiệt độ (ºC) | Tần suất (%) | Giá trị đại diện |
| [15; 17] | 16,7 | 16 |
| [17; 19) | 43,3 | 18 |
| [19; 21) | 36,7 | 20 |
| [21; 23] | 3,3 | 22 |
| Cộng | 100 (%) |
Số trung bình cộng của bảng 6 là:
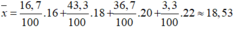
Số trung bình cộng của bảng 8 là:
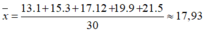
b) Nhiệt độ trung bình của thành phố Vinh trong tháng 12 cao hơn nhiệt độ trung bình trong tháng 2 khoảng 0,6ºC.

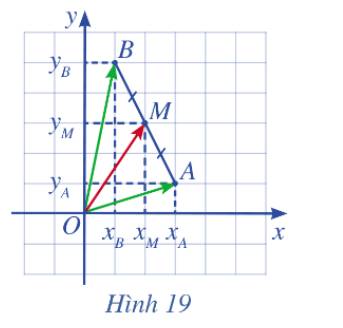
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

a) \(23,3\) phút; \(540^0;27,6^0C\)
b) Khi lấy số trung bình làm đại diện cho các số liệu thống kê về quy mô và độ lớn, có thể xem rằng mỗi ngày bạn A đi từ nhà đến trường đều mất 23,3 phút.
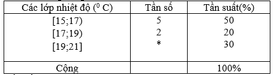
Tương tự, nêu ý nghĩa số trung bình của các số liệu thống kê cho ở bảng 7 và bảng 8.

Từ năm 1991 đến hết năm 2000 là có 10 năm. Do đó kích thước mẫu là 10.
Dựa vào bảng thống kê ta có: n1= 5; n2= 2
Do đó n3= N – n1- n2 = 10- 5-2=3
Chọn B.

a) Diện tích rừng trung bình của nước ta từ năm 2008 đến năm 2019 là: \(\overline X = \frac{{13,1 + 13,2 + 13,4 + 13,5 + 13,9 + 14,0 + 13,8 + 14,1 + 14,4 + 14,4 + 14,5 + 14,6}}{{12}} = 13,9\)
b) Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị thấp nhất là: 13,1 (ha)
Từ năm 2008 đến năm 2019, diện tích rừng của năm có giá trị cao nhất là: 14,6 (ha)
c) +) So với năm 2008, tổng diện tích rừng của nước ta năm 2019 tăng lên số héc-ta là: \(\Delta = 14,6 - 13,1 = 1,5\left( {ha} \right)\)
Vậy so với năm 2008, tỉ lệ tổng diện tích rừng của nước ta năm 2019 tăng lên được : \(\frac{{1,5}}{{13,1}} = 11,4\% \)
Theo em, tỉ lệ cây tăng đó là cao.

Nhiệt độ trung bình của tháng 5 ở địa phương A từ 1961 đến hết 1990
| Lớp nhiệt độ (
C
0
) |
Tần số | Tần suất (%) |
| [25; 26) | 1 | 3,3 |
| [26; 27) | 5 | 16,7 |
| [27; 28) | 13 | 43,3 |
| [28; 29) | 9 | 30,0 |
| [29; 30] | 2 | 6,7 |
| Cộng | 30 | 100 (%) |








a) Nhiệt độ trung bình trong năm ở Hà Nội là: \(\overline X = \frac{{16,4 + 17,0 + 20,2 + 23,7 + 27,3 + 28,8 + 28,9 + 28,2 + 27,2 + 24,6 + 21,4 + 18,2}}{{12}} = 23,5\)
b) Nhiệt độ trung bình của tháng có giá trị thấp nhất là: \(16,4\left( {^oC} \right)\)
Nhiệt độ trung bình của tháng có giá trị cao nhất là: \(28,9\left( {^oC} \right)\)