Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bình không đạt giải nhất, nhì, ba => Bình đạt giải khuyến khích
An không đạt giải nhất, nhì, ba => An đạt giải khuyến khích
Cường không đạt giải nhất, ba, khuyến khích => Cường đạt giải nhì
Đông không đạt giải nhất, ba khuyến khích => Đông đạt giải nhì

bài 2
1)
/2x-7/+\(\dfrac{1}{2}=1\dfrac{1}{2}\)
/2x-7/+\(\dfrac{1}{2}=\dfrac{3}{2}\)
/2x-7/=1
=> 2x-7=1 hoặc -2x+7 =1
2x=8 hoặc -2x=-6
x=4 hoặc x=3
Bài 1:
1: Ta có: \(A=\left(-1\right)^3\cdot\left(-\dfrac{7}{8}\right)^3\cdot\left(-\dfrac{2}{7}\right)^2\cdot\left(-7\right)\cdot\left(-\dfrac{1}{14}\right)\)
\(=\dfrac{7^3}{8^3}\cdot\dfrac{4}{49}\cdot\dfrac{1}{2}\)
\(=\dfrac{343}{512}\cdot\dfrac{2}{49}\)
\(=\dfrac{7}{256}\)

Lời giải:
$4+(y-1)^2\geq 4\Rightarrow \frac{8}{4+(y-1)^2}\leq 2$
Mặt khác, áp dụng BĐT $|a|+|b|\geq |a+b|$ ta có:
$|x-1|+|x-3|=|x-1|+|3-x|\geq |x-1+3-x|=2$
$\Rightarrow |x-1|+|x-2|+|x-3|\geq 2+|x-2|\geq 2$
Vậy $\frac{8}{4+(y-1)^2}\leq 2\leq |x-1|+|x-2|+|x-3|$
Dấu "=" xảy ra khi:
\(\left\{\begin{matrix} (y-1)^2=0\\ (x-1)(3-x)\geq 0\\ x-2=0\end{matrix}\right.\Leftrightarrow y=1; x=2\)

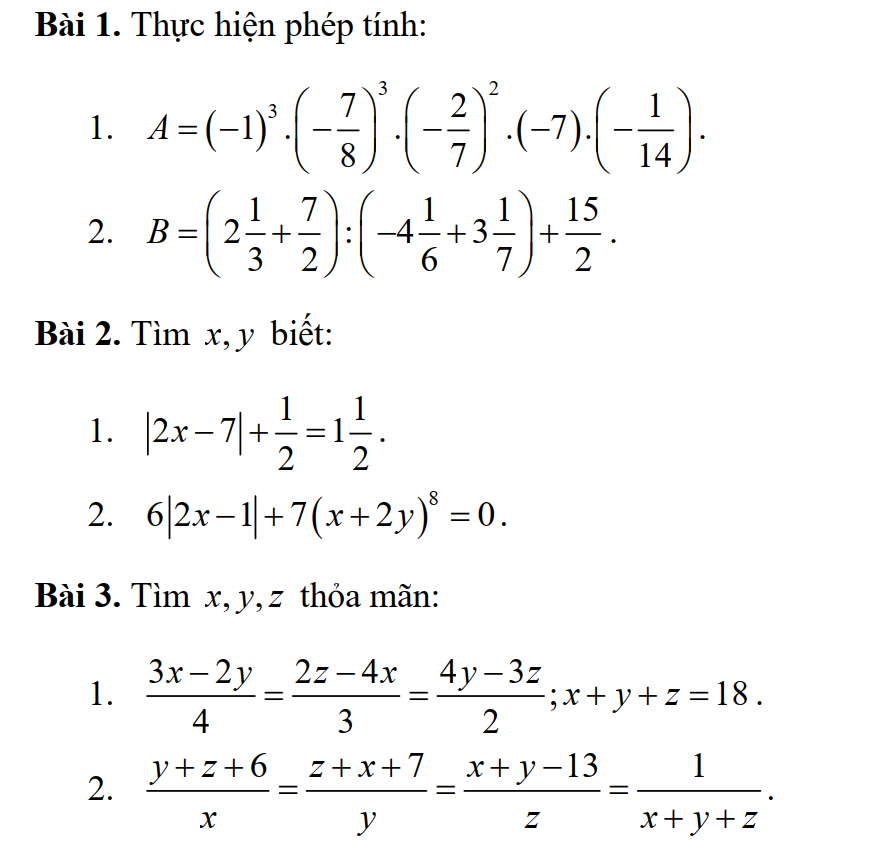
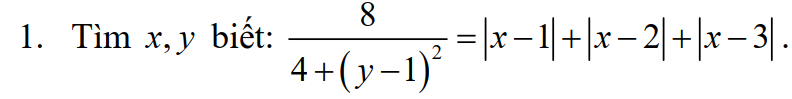
 Mình có 4 bài toán về xích ma . Nhờ các bạn hướng dẫn khai triển giúp mình với . Và có cách nào khai triển bằng máy tính casio không ạ ?
Mình có 4 bài toán về xích ma . Nhờ các bạn hướng dẫn khai triển giúp mình với . Và có cách nào khai triển bằng máy tính casio không ạ ?
Đề:01
Câu 1. (2.5 điểm)
a) Phát biểu định lí về tổng ba góc của một tam giác?
b) Áp dụng: MNP cân tại P. Biết góc N có số đo bằng 500. Tìm số đo góc P?
Câu 2. (2.5 điểm)
a) Phát biểu định lí Pytago?
b) Áp dụng: HIK vuông tại H có các cạnh góc vuông là 3cm; 4cm. Độ dài cạnh huyền IK bằng bao nhiêu?
Câu 4. (5 điểm)
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC (H BC)
a) Chứng minh HB = HC
b) Chứng minh
c) Kẻ HD vuông góc với AB (D AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân.
Đề 02:
Câu 1: (2.5 điểm)
a. Phát biểu định lý Pytago đảo ?
b. Kiểm tra xem tam giác có ba cạnh lần lượt là 12 cm, 13 cm, 5 cm có phải là độ dài 3 cạnh của tam giác vuông hay không?
Câu 2: Tam giác ABC vuông tại B.
a. Độ dài hai cạnh góc vuông là AB, BC lần lượt là: . Tính độ dài AC ?
b. Cạnh huyền AC là 5 cm và cạnh BC là 4 cm. Tính độ dài cạnh AB ?
Câu 3: Câu 4. (5 điểm)
Cho tam giác MNP cân tại M. Kẻ MH vuông góc với NP (H NP)
a) Chứng minh HP = HN
b) Chứng minh
c) Kẻ HD vuông góc với AB (D AB). Kẻ HE vuông góc với AC (E AC). Chứng minh tam giác HDE là tam giác cân.
thi tốt nha!
tks bn!!!!!!!!!