Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

+)Muốn tính \(\cot\) bằng máy tính, bạn ấn \(\dfrac{1}{\tan\left(...\right)}\) (...) là số đo góc
Từ số ra góc thì bạn ấn Shift + nút \(\sin,\cos,\tan\) rồi nhập tỉ số lượng giác vô thì ra số đo góc nha
+)\(\sin^2x=\sin x\cdot\sin x;\sin x^2=\sin\left(x\cdot x\right)\)
\(\Rightarrow\sin^2x\ne\sin x^2\)

zô fx, xóa \(y=\frac{1}{x^2+\sqrt{x}}\), , cái đầu tiên là căn bậc 2 \(\sqrt{ }\)
ok bn ^^

Ta có : \(\dfrac{x}{y}=\dfrac{1}{2}\)
\(\Leftrightarrow2x=y\)
\(\Leftrightarrow2x-y=0\)
Theo bài ra ta có hệ : \(\left\{{}\begin{matrix}12x+y=42\\2x-y=0\end{matrix}\right.\)
CASIO fx-580VNX ( Ko bt bạn dùng loại nào mk lấy đại diện :vvv )
ON - MENU SETUP - 9 - 1 - 2 - Nhập số = Nhập số = .... = x = 3 = y = 6 .
Vậy ...
Ta có: \(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{1}{2}\\12x+y=42\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2x\\12x+2x=42\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=42\\y=2x\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\cdot3=6\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là (x,y)=(3;6)


Bạn hình như chép nhầm đề rồi
\(4=\sqrt{16};2\sqrt{15}=\sqrt{60}\)
Sao trừ trong căn được

Tại sao không giải ra $\sqrt{P}$ và $\sqrt{P}$?
Em đã có $P$ rồi, nhưng với $\sqrt{P}$, em làm sao rút gọn được khi mà $P$ đã khá gọn rồi. Cũng chẳng có giá trị nào của $x$ để tính cụ thể $P, \sqrt{P}$ rồi đi so sánh. Vì vậy cách này không khả thi.
Vậy thì phải tìm hướng khác. Muốn so sánh 2 số, ta xét hiệu hai số đó.
$P-\sqrt{P}=\sqrt{P}(\sqrt{P}-1)$
Rõ ràng $\sqrt{P}$ đã dương rồi, giờ ta phải xem xét xem $\sqrt{P}-1$ âm hay dương, hay $P$ có lớn hơn 1 không
Đó là lý do vì sao bài giải như trên.
Còn câu hỏi khi nào giải ra từng cái $P$ và $\sqrt{P}$, thì đó là khi đề cho $x=2$ chả hạn, so sánh $P$ và $\sqrt{P}$.
Nhưg hầu như sẽ chẳng có đề nào ra kiểu vậy, mà đa số lợi dụng tính chất của phân thức đó để so sánh (ví dụ như trong bài tính chất nổi bật là $P>1$) cho nhanh. Đó là cái hay của đề bài.
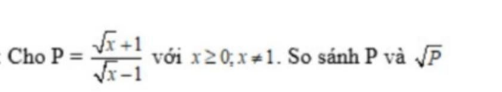
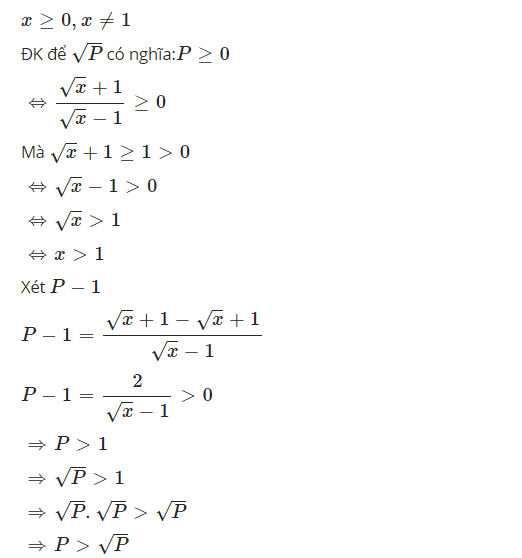
Pạn bấm zào chữ fx trên thanh công cụ → xóa những cái hiện lên rồi cứ bấm 1/2
\(\frac{1}{2}\)