Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Phản ứng thu năng lượng nên ta có: ∆ E = K p + K α - K α = - 2 , 7 M e V ( 1 )
Vì hai hạt tạo thành bay ra với cùng vận tốc nên ta có:
K P K n = m p m n = 30 ( 2 )
Bảo toàn động lượng: P α = P P + P n vì hai hạt bay ra với cùng vận tốc nên ta có:
P α = P P + P n hay 2 m α K α = 2 m p K p + 2 m n K n ( 3 )
Thay (2) vào (3) ta sẽ được:
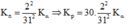
Thay các giá trị vào (1) ta sẽ tính được: K α = 3 , 1 M e V

Phương pháp:
Sử dụng định luật bảo toàn điện tích và số khối để viết phương trình phản ứng hạt nhân
Sử dụng định luật bảo toàn động lượng; định lí hàm số cos trong tam giác
Năng lượng toả ra của phản ứng Q = Ks – Kt (Kt và Ks lần lượt là tổng động năng của các hạt trước và sau phản ứng hạt nhân.

Cách giải:
Phương trình phản ứng hạt nhân: p 1 1 + Li 3 7 → 2 He 2 4
Năng lượng toả ra của phản ứng: Q = 2Kα – Kp
Kp = 5,5 MeV
Định luật bảo toàn động lượng: p p → = p α 1 → + p α 2 →
Áp dụng định lí hàm số cos ta có:
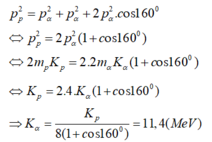
Þ Năng lượng toả ra của phản ứng: Q = 17,3 (MeV)
Đáp án C

\(_1^1p + _4^9Be \rightarrow _2^4He + _3^6X\)
Áp dụng định luật bảo toàn động lượng \(\overrightarrow P_p+0 =\overrightarrow P_{He}+ \overrightarrow P_{X} \)(hạt nhân Be đứng yên)
Dựa vào hình vẽ ta có
P P P He X p
\(P_{p}^2+ P_{He}^2 = P_X^2\)
=> \(2m_{p}K_{p}+2m_{He} K_{He} = 2m_{X}K_{X}. \)
=> \(K_{p}+4K_{He} = 6K_{X} => K_X = 3,575MeV.\)
Áp dụng định luật bảo toàn năng lượng toàn phần (hạt nhân Be đứng yên)
\(K_{p}+m_{p}c^2+m_{Be}c^2 = K_{He} + m_{He}c^2+ K_{X}+m_{X}c^2\)
=> \((m_p-m_{He}-m_{X})c^2= K_{He}+K_X-K_p= 2,125MeV\)
Như vậy năng lượng tỏa ra của phản ứng chính bằng hiệu động năng của các hạt sau phản ứng cho động năng của các hạt trước phản ứng và bằng 2,125 MeV.

Đáp án B
Phương pháp: Áp dụng định luật bảo toàn động năng và động lượng
Cáchgiải: Đáp án B
Ta có
![]()
![]()
giản đồ vecto
![]()
gọi b là góc hợp bởi hướng lệch của hạt X so với hướng chuyển động của hạt α ta có
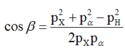
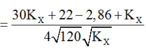
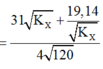




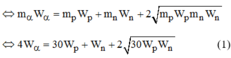
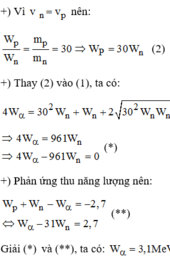

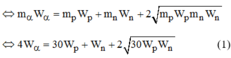
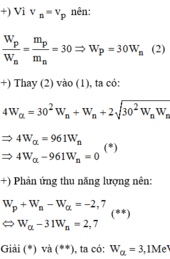
\(_2^4 He + _{13}^{27}Al \rightarrow _{15}^{30}P + _0^1n\)
Phản ứng thu năng lượng
\( K_{He} - (K_{P}+K_{n} )= 2,7MeV.(*)\)
Lại có \(\overrightarrow v_P = \overrightarrow v_n .(1)\)
=> \(v_P = v_n\)
=> \(\frac{K_P}{K_n} = 30 .(2)\)
Áp dụng định luật bảo toàn động lượng trước và sau phản ứng
\(\overrightarrow P_{He} = \overrightarrow P_{P} + \overrightarrow P_{n} \)
Do \(\overrightarrow P_{P} \uparrow \uparrow \overrightarrow P_{n}\)
=> \(P_{He} = P_{P} + P_{n} \)
=> \(m_{He}.v_{He} = (m_{P}+ m_n)v_P=31m_nv\) (do \(v_P = v_n = v\))
=> \(K_{He} = \frac{31^2}{4}K_n.(3)\)
Thay (2) và (3) vào (*) ta có
\(K_{He}-31K_n= 2,7.\)
=> \(K_{He} = \frac{2,7}{1-4/31} = 3,1MeV.\)
Khe=31^2/4Kn lam sao ra dc nhu the a