Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trường hợp xấu nhất là bạn A lấy ra cả 1 quả đen, 2 quả xanh, 2 quả vàng, 2 quả trắng, 2 quả đỏ rồi bạn A mới lấy được 1 quả đỏ, trắng hay vàng để được 3 quả cùng màu.
Vậy số quả bóng cần lấy ra ít nhất để có 3 quả cùng màu là: 1 + 2 + 2 + 2 + 2 + 1 = 10 (quả)
ĐS: 10 quả

Chọn C.
Phương pháp:
Sử dụng kiến thức về tổ hợp và hai qui tắc đếm cơ bản.
Chia các trường hợp có thể xảy ra để tìm kết quả.
Cách giải:
Lấy ngẫu nhiên 5 quả cầu mà số quả cầu xanh lớn hơn số quả cầu đỏ ta có các trường hợp sau :
TH1: 5 quả cầu xanh, 0 quả cầu đỏ thì số cách chọn là C 5 5 (cách)
TH2 : 4 quả cầu xanh, 1 quả cầu đỏ thì số cách chọn là C 5 4 . C 7 1 (cách)
TH3 : 3 quả cầu xanh, 2 quả cầu đỏ thì số cách chọn là C 5 3 . C 7 2 (cách)
Vậy số cách chọn thỏa mãn đề bài là C 5 5 + C 5 4 . C 7 1 + C 5 3 . C 7 2 =246 (cách)

Đáp án C
Phương pháp:
Chia thành các trường hợp:
+ Trong hai quả bóng bốc được có ít nhất một quả có số chia hết cho 10.
+ Trong hai quả bốc được có một quả có chữ số hàng đơn vị bằng 5 và một quả có chữ số hàng đơn vị là 2,4,6,8.
Đếm số khả năng có lợi cho biến cố và tính xác suất.
Cách giải:
Xét phép thử T: “Bốc ngẫu nhiên 2 trong 50 quả bóng”.
Số phần tử không gian mẫu n Ω = C 50 2
Gọi A là biến cố: “Tích hai số ghi trên hai bóng chia hết cho 10:.
+) TH1: Trong hai quả bốc được có ít nhất 1 quả có số chia hết cho 10
Số cách chọn để trong hai quả không có quả nào có số chia hết cho 10 là C 45 2
→ Số cách chọn để trong hai quả có ít nhất 1 quả có số chia hết cho 10 là
![]()
+) TH2: Trong hai quả bốc được có 1 quả có chữ số hàng đơn vị là 5 và 1 quả có chữ số hàng đơn vị là 2,4,6,8.
Số cách chọn để có được hai số trên (không phân biệt thứ tự) là
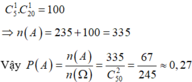

Chọn đáp án B
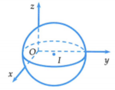
Hai bức tường và nền nhà mà quả bóng tiếp xúc tạo thành một hệ trục tọa độ Oxyz như hình vẽ. Mỗi quả bóng coi như một mặt cầu có tâm I a ; b ; c
Vì mỗi quả bóng đều tiếp xúc với hai bức tường và nền nhà nên chúng tiếp xúc với ba mặt phẳng tọa độ O x y , O y z v à O x z
Tức là
![]()
![]()
Suy ra I a ; a ; a
Gọi M x ; y ; z là điểm nằm trên quả bóng có khoảng cách đến hai bức tường và nền nhà mà nó tiếp xúc bằng 1, 2, 4
Suy ra M 1 ; 2 ; 4
Điểm M nằm trên quả bóng khi
![]()
![]()
Phương trình (*) có ∆ ' = 7 > 0 nên có hai nghiệm a 1 , a 2 và a 1 + a 2 = 7 (theo định lý Vi-ét). Khi đó tổng đường kính của hai quả bóng là
2 a 1 + a 2 = 14

Đáp án B.
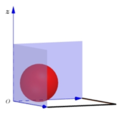
Phương pháp giải: Gắn hệ tọa độ Oxyz, tìm bán kính quả bóng chính là bán kính của mặt cầu
Lời giải: Xét quả bóng tiếp xúc với các bức tường và chọn hệ trục Oxyz như hình vẽ bên (tương tự với góc tường còn lại).
Gọi I(a;a;a) là tâm của mặt cầu (tâm quả bóng) và R = a
=> phương trình mặt cầu của quả bóng là ![]()
Giả sử M(x;y;z) nằm trên mặt cầu (bề mặt của quả bóng) sao cho d(M;(Oxy)) = 1; d(M;(Oyz)) = 2; d(M;(Oxz)) = 3
Khi đó z = 1; x = 2; y = 3 => M(2;3;1) ∈ (S) (2).
Từ (1),(2) suy ra ![]()
=>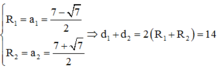

Đáp án C
Số khả năng lấy được số quả đỏ nhiều hơn số quả cầu xanh là:
![]()

Chọn C.
Lấy ngẫu nhiên 5 quả cầu từ hộp 12 quả cầu, để số quả cầu đỏ nhiều hơn số quả xanh, những trường hợp có thể xảy ra là:
Trường hợp 1: 5 quả cầu đỏ
Số khả năng: C 5 5 = 1 khả năng.
Trường hợp 2: 4 cầu đỏ, 1 cầu xanh
Số khả năng: C 5 4 . C 7 1 = 35 khả năng.
Trường hợp 3: 3 cầu đỏ, 2 cầu xanh
Số khả năng: C 5 3 . C 7 2 = 210 khả năng.
Áp dụng quy tắc cộng có tất cả: 35 + 210 + 1= 246 khả năng.

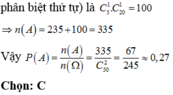


- Nhặt 6 quả và đặt lên cân mỗi bên 3 quả,nếu cân bằng => quả bóng nặng hơn nằm trong số 2 quả còn lại. Ta chỉ cần đặt 2 quả còn lại lên cân là có thể tìm ra quả bóng nặng.
- Nếu quả bóng nặng hơn nằm trong số 6 quả mà ta đặt lên cân, ta sẽ loại xuống được còn 3 quả. Trong số 3 quả đó, đặt 2 quả bóng lên cân. Nếu chúng bằng nhau => quả nặng nhất là quả còn lại.