Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời :
\(\frac{2004.2004+3006}{2005.2005-1003}\)\(=\)\(\frac{4016016+3006}{4020025-1003}\)
\(=\)\(\frac{4019022}{4019022}\)
\(=\)\(1\)

1/
a) ta có \(\dfrac{1}{1.4}+\dfrac{1}{4.7}+...+\dfrac{1}{97.100}=\dfrac{1}{3}.\left(\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{97.100}\right)\)
\(=\dfrac{1}{3}.\left(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{10}+...+\dfrac{1}{97}-\dfrac{1}{100}\right)\)
\(=\dfrac{1}{3}.\dfrac{99}{100}=\dfrac{33}{100}\)
⇒ \(\dfrac{33}{100}=\dfrac{0,33x}{2009}\)
⇒ \(\dfrac{33}{100}=\dfrac{0,33}{2009}.x\Rightarrow x=\dfrac{33}{100}:\dfrac{0,33}{2009}=2009\)
b,1 + 1/3 + 1/6 + 1/10 + ... + 2/x(x+1)=1 1991/1993
2 + 2/6 + 2/12 + 2/20 + ... + 2/x(x+1) = 3984/1993
2.(1/1.2 + 1/2.3 + 1/3.4 + ... + 1/x(x+1) = 3984/1993
2.(1 − 1/2 + 1/2 − 1/3 + ... + 1/x − 1/x+1)=3984/1993
2.(1 − 1/x+1) = 3984/1993
1 − 1/x + 1= 3984/1993 :2
1 − 1/x+1 = 1992/1993
1/x+1 = 1 − 1992/1993
1/x+1=1/1993
<=>x+1 = 1993
<=>x+1=1993
<=> x+1=1993
<=> x = 1993-1
<=> x = 1992

1/ \(B=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{8^2}\)
\(B< \dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{7.8}\)
\(B< \dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{7}-\dfrac{1}{8}\)
\(B< \dfrac{1}{1}-\dfrac{1}{8}< 1\)
\(B< 1\)
2/ \(B=\left(1-\dfrac{1}{2}\right)\left(1-\dfrac{1}{3}\right)\left(1-\dfrac{1}{4}\right)...\left(1-\dfrac{1}{20}\right)\)
\(B=\dfrac{1}{2}\cdot\dfrac{2}{3}\cdot\dfrac{3}{4}\cdot...\cdot\dfrac{19}{20}\)
\(B=\dfrac{1\times2\times3\times...\times19}{2\times3\times4\times...\times20}\)
\(B=\dfrac{1}{20}\)
3/ \(A=\dfrac{7}{4}\cdot\left(\dfrac{3333}{1212}+\dfrac{3333}{2020}+\dfrac{3333}{3030}+\dfrac{3333}{4242}\right)\)
\(A=\dfrac{7}{4}\cdot\left(\dfrac{33}{12}+\dfrac{33}{20}+\dfrac{33}{30}+\dfrac{33}{42}\right)\)
\(A=\dfrac{7}{4}\cdot\left(\dfrac{33}{3.4}+\dfrac{33}{4.5}+\dfrac{33}{5.6}+\dfrac{33}{6.7}\right)\)
\(A=\dfrac{7}{4}.33.\left(\dfrac{1}{3}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{7}\right)\)
\(A=\dfrac{231}{4}.\left(\dfrac{1}{3}-\dfrac{1}{7}\right)\)
\(A=\dfrac{231}{4}\cdot\dfrac{4}{21}\)
\(A=11\)
4/ A phải là \(\dfrac{2011+2012}{2012+2013}\)
Ta có : \(B=\dfrac{2011}{2012}+\dfrac{2012}{2013}>\dfrac{2011}{2013}+\dfrac{2012}{2013}=\dfrac{2011+2012}{2013}>\dfrac{2011+2012}{2012+2013}=A\)
\(\Rightarrow B>A\)

a) \(2^x+2^{x+1}+2^{x+2}+2^{x+3}=480\)
\(\Rightarrow\)\(2^x+2^x.2+2^x.2^2+2^x.2^3=480\)
\(\Leftrightarrow\)\(2^x\left(1+2+2^2+2^3\right)=480\)
\(\Leftrightarrow\)\(2^x\left(1+2+4+8\right)=480\)
\(\Leftrightarrow\)\(2^x.15=480\)
\(\Rightarrow\)\(2^x=480:15\)
\(\Leftrightarrow2^x=32\)
\(\Rightarrow2^x=2^5\)
\(\Rightarrow x=5\)
Vậy x = 5.

\(A=\dfrac{2013}{1}+\dfrac{2012}{2}+\dfrac{2011}{3}+...+\dfrac{1}{2013}\)
\(=\left(\dfrac{2012}{2}+1\right)+\left(\dfrac{2011}{3}+1\right)+...+\left(\dfrac{1}{2013}+1\right)+1\)
\(=\dfrac{2014}{2}+\dfrac{2014}{3}+...+\dfrac{2014}{2013}+\dfrac{2014}{2014}\)
\(=2014\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2013}+\dfrac{1}{2014}\right)\)
\(P=\dfrac{2013}{2}+\dfrac{2013}{3}+...+\dfrac{2013}{2014}=2013\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2014}\right)\)
\(\Rightarrow\dfrac{P}{A}=\dfrac{2013\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2014}\right)}{2014\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2014}\right)}=\dfrac{2013}{2014}\)
Vậy \(\dfrac{P}{A}=\dfrac{2013}{2014}\)

1.Tính hợp lý:
a. 1152 - (374 + 1152) + (374 - 65) = 1152 - 374 - 1152 + 374 - 65 = ( 1152 - 1152 ) + ( -65) + ( 374 - 374 ) = 0 + ( - 65) + 0 = -65
Bài 1 : Tính hợp lý : c. \(\dfrac{11.3^{22}.3^7-9^{15}}{\left(2.3^{14}\right)^2}\) = \(\dfrac{11.3^{29}-3^{30}}{2^2.3^{28}}\) = \(\dfrac{3^{29}.\left(11-3\right)}{2^2.3^{28}}\) = \(\dfrac{3^{29}.2^3}{2^2.3^{28}}\) = 6
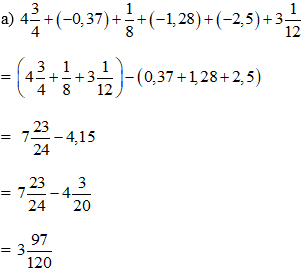
\(A=\dfrac{1995.1994-1}{1993.1995+1994}=\dfrac{1995\left(1993+1\right)-1}{1993.1995+1994}=\dfrac{1995.1993+1995-1}{1993.1995+1994}=\dfrac{1995.1993+1994}{1995.1993-1994}=1\)\(B=\dfrac{2004.2004+3006}{2005.2005-1003}=\dfrac{2004.2004+2004.1+1002}{2005.2005-1003}=\dfrac{2004.2005+1002}{2005.2005-1003}=\dfrac{2004.2005+1002}{2004.2005+2005-1003}=\dfrac{2004.2005+1002}{2004.2005+1002}=1\)\(C=\dfrac{2010.2011-1}{2009.2011+2010}=\dfrac{2009.2011+2011-1}{2009.2011+2010}=\dfrac{2019.2011+2010}{2009.20011+2010}=1\)\(D=\dfrac{2014.2015-1}{2013.2015+2013}=\dfrac{2013.2015+2014-1}{2013.2015+2013}=\dfrac{2013.2015+2013}{2013.2015+2013}=1\)
Câu 1 nhầm đề nha bạn mình sửa:
\(\dfrac{1995.1994-1}{1993.1995+1994}\)
\(=\dfrac{1995.\left(1993+1\right)-1}{1993.1995+1994}\)
\(=\dfrac{1995.1993+1995-1}{1993.1995+1994}\)
\(=\dfrac{1993.1995+1994}{1993.1995+1994}\)
\(=1\)
Câu 2: \(\dfrac{2004.2004+3006}{2005.2005-1003}\)
\(=\dfrac{2004.2004+2004+1002}{\left(2004+1\right).\left(2004+1\right)-1003}\)
\(=\dfrac{2004.2004+2004+1002}{2004.2004+2004+1-1003}\)
\(=\dfrac{2004.2004+2004+1002}{2004.2004+2004+1002}\)
\(=1\)
Câu 3:\(\dfrac{2010.2011-1}{2009.2011+2010}\)
\(=\dfrac{\left(2009+1\right).2011-1}{2009.2011+2010}\)
\(=\dfrac{2009.2011+2011-1}{2009.2011+2010}\)
\(=\dfrac{2009.2011+2010}{2009.2011+2010}\)
= 1
Câu 4:Nhầm để, sửa:
\(\dfrac{2014.2015-1}{2013.2015+2014}\)
\(=\dfrac{\left(2013+1\right).2015-1}{2013.2015+2014}\)
\(=\dfrac{2013.2015+2015-1}{2013.2015+2014}\)
\(=\dfrac{2013.2015+2014}{2013.2015+2014}\)
\(=1\)