
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

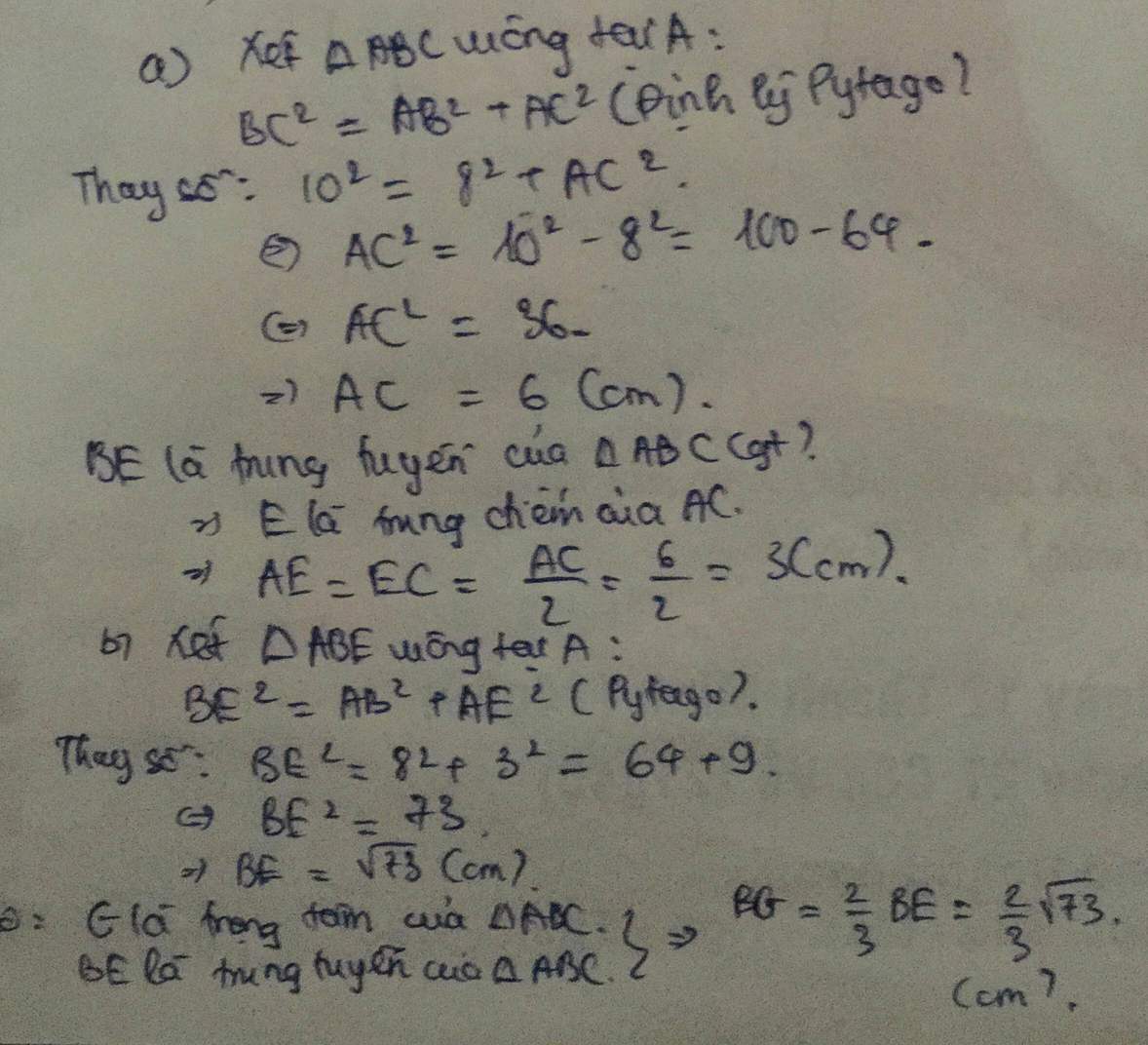

B2:
1)Áp dụng định lý Py-ta-go vào tam giác vuông ABC,ta có
BC^2=AB^2+AC^2
\Leftrightarrow10^2=8^2+AC^2
\LeftrightarrowAC^2=10^2-8^2
\LeftrightarrowAC^2=100-64
\LeftrightarrowAC^2=36
\RightarrowAC=6cm(đpcm)
Mà BE là trung tuyến của cạnh AC
\RightarrowAE=6/2=3cm(đpcm)

bạn ơi mình chỉ tính câu a) tính AC thoy nha rồi bạn dựa vào nha:
\(\Delta\)ABC vuông tại A, có:
\(BC^2=AB^2+AC^2\)
\(10^2=8^2+AC^2\)
\(AC^2=10^2-8^2\)
\(AC^2=100-64\)
\(AC^2=36\)
\(AC=\sqrt{36}=6cm\)

a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC^2=10^2-8^2=36\)
hay AC=6(cm)
Ta có: E là trung điểm của AC
nên \(AE=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b: Áp dụng định lí Pytago vào ΔABE vuông tại A, ta được:
\(BE^2=BA^2+AE^2\)
\(\Leftrightarrow BE^2=3^2+8^2=73\)
hay \(BE=\sqrt{73}\left(cm\right)\)
Xét ΔABC có
AD là đường trung tuyến ứng với cạnh BC
BE là đường trung tuyến ứng với cạnh AC
AD cắt BE tại G
Do đó: G là trọng tâm của ΔABC
Suy ra: \(BG=\dfrac{2}{3}BE=\dfrac{2\sqrt{73}}{3}\left(cm\right)\)

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AC^2=10^2-8^2=36\)
hay AC=6(cm)
Ta có: E là trung điểm của AC(gt)
nên \(AE=\dfrac{AC}{2}=\dfrac{6}{2}=3\left(cm\right)\)
b) Áp dụng định lí Pytago vào ΔABE vuông tại A, ta được:
\(BE^2=AB^2+AE^2\)
\(\Leftrightarrow BE^2=8^2+3^2=73\)
hay \(BE=\sqrt{73}\left(cm\right)\)
Xét ΔABC có
BE là đường trung tuyến ứng với cạnh AC(gt)
AD là đường trung tuyến ứng với cạnh BC(gt)
BE cắt AD tại G
Do đó: G là trọng tâm của ΔABC(Tính chất ba đường trung tuyến của tam giác)
Suy ra: \(BG=\dfrac{2}{3}BE=\dfrac{2}{3}\cdot\sqrt{73}=\dfrac{2\sqrt{73}}{3}\left(cm\right)\)

a: \(AC=\sqrt{10^2-8^2}=6\left(cm\right)\)
nên AE=3(cm)
b: \(BE=\sqrt{8^2+3^2}=\sqrt{73}\left(cm\right)\)
\(BG=\dfrac{2\sqrt{73}}{3}\left(cm\right)\)