Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

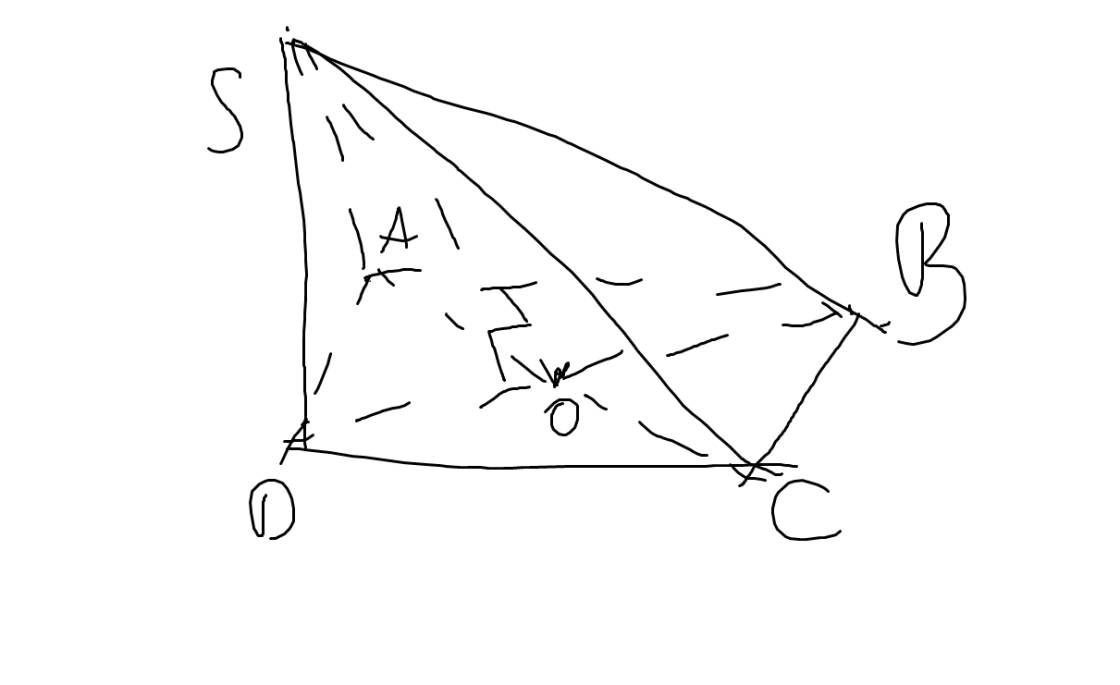
Trong hình chóp tứ giác đều, đường cao kẻ từ đỉnh xuống đáy có chân đường cao là tâm của đáy và đường cao đó chính là trung đoạn của hình chóp
a: Vẽ SO\(\perp\)(ABCD)
=>SO là trung đoạn của hình chóp ABCD và O là tâm của hình vuông ABCD
=>O là trung điểm chung của AC và BD
ABCD là hình vuông
=>\(AC=BD=\sqrt{4^2+4^2}=4\sqrt{2}\left(cm\right)\)
=>\(AO=BO=CO=DO=\dfrac{4\sqrt{2}}{2}=2\sqrt{2}\left(cm\right)\)
SO vuông góc (ABCD)
=>SO vuông góc OD
=>ΔSOD vuông tại O
=>\(SO^2+OD^2=SD^2\)
=>\(SO^2=6^2-8=28\)
=>\(SO=2\sqrt{7}\left(cm\right)\)
b: \(S_{Xq}=p\cdot d=C_{đáy}\cdot SO=4\cdot4\cdot2\sqrt{7}=32\sqrt{7}\left(cm^2\right)\)
c: \(S_{tp}=S_{xq}+S_{đáy}\)
\(=32\sqrt{7}+4^2=32\sqrt{7}+16\left(cm^2\right)\)

Đề đúng rồi. Chỉ tiếc là ko biết cách giải. Đáp số là :4,8cm
toi can cau hoi khac .Do bai nay kho qua ,khong biet lam.Hieu chua.

Diện tích tg ABC là :
\(\frac{1}{2}.AC.AB=\frac{1}{2}.7.6=21\left(cm^2\right)\)
Vậy:........
#H

Nửa chu vi tam giác:
\(\dfrac{\left(10+17+21\right)}{2}=24\left(cm\right)\)
Diện tích tam giác:
\(S=\sqrt{24.\left(24-10\right).\left(24-17\right).\left(24-21\right)}=84\left(cm^2\right)\)
Xét Δ𝐴𝐵𝐶ΔABC có 𝐴𝐵=10AB=10 cm, 𝐴𝐶=17AC=17 cm, 𝐵𝐶=21BC=21 cm.
Gọi 𝐴𝐻AH là đường cao của tam giác.
Vì 𝐵𝐶BC là cạnh lớn nhất của tam giác nên 𝐵^,𝐶^<90∘B,C<90∘, do đó 𝐻H nằm giữa 𝐵B và 𝐶C.
Đặt 𝐻𝐶=𝑥,𝐻𝐵=𝑦HC=x,HB=y, ta có : 𝑥+𝑦=21x+y=21 (1)
Mặt khác 𝐴𝐻2=102−𝑦2,𝐴𝐻2=172−𝑥2AH2=102−y2,AH2=172−x2 nên 𝑥2−𝑦2=172−102=289−100=189x2−y2=172−102=289−100=189 (2)
Từ (1) và (2) suy ra 𝑥+𝑦=21x+y=21, 𝑥−𝑦=9x−y=9.
Do đó 𝑥=15x=15, 𝑦=6y=6.
Ta có 𝐴𝐻2=102−62=64AH2=102−62=64 nên 𝐴𝐻=8AH=8.
Vậy 𝑆𝐴𝐵𝐶=21.82=84SABC=221.8=84 (cm22).