Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H 7 cm 2 cm 2 cm
Ta có: AC = AH + HC = 7 + 2 = 9 (cm)
Vì AB = AC => AB = 9 cm
Áp dụng định lí Pi - ta - go vào t/giác AHB vuông tại H, ta có:
AB2 = AH2 + BH2
=> BH2 = AB2 - AH2 = 92 - 72 = 32
Áp dụng định lí Pi - ta - go vào t/giác AHC vuông tại H, ta có:
BC2 = BH2 + HC2 = 32 + 22 = 36
=> BC = 6 (cm)

Xét tam giác BAH
Có B+BAH=900(vì tam giác BAH vuông tại H)
500+BAH=900
=>BAH=900-500
=>BAH=400
Xét tam giác HAC
Có C+HAC=900(Tam giác HAC vuông tại H)
400+HAC= 900
HAC=900-400
HAC=500
B)Xét tam giác ABH
Có AB2 = HB2+AH2(Theo định lý Pi-ta-go)
AB2=32+42
AB2=25=52
AB=5
Xét tam giác CAH
Có AC2=AH2+HC2 (Theo định lý Pi-ta-go)
AC2=42+42=32=

A B C D E H
a, Xét \(\Delta ABH\) và\(\Delta ACH\) CÓ:
\(AHchung\)
AB = AC
\(\widehat{AHB}=\widehat{AHC}\)
\(\Rightarrow\Delta ABH=\Delta ACH\)(cạnh huyền cạnh góc vuông)
=> BH = HC ( 2 cạnh tương ứng )
b,Do BC = 8cm => BH = 4cm
Áp dụng định lý Py ta go vào tam giác vuông ABH có :
\(AH^2+BH^2=AB^2\)
\(\Rightarrow AH^2=AB^2-BH^2\)\(\Rightarrow AH^2=5^2-4^2=25-16=9\)\(\Rightarrow AH=3\left(cm\right)\)
c,\(Xét\Delta DBH\) và\(\Delta ECH\) có :
\(\widehat{ABH}=\widehat{ACH}\)
BH = HC
\(\widehat{BDH}=\widehat{CEH}\)
\(\Rightarrow\Delta DBH=\Delta ECH\)\(\Rightarrow DH=EH\)=> \(\Delta DHE\) cân tại H
cho mình 1 tym nha
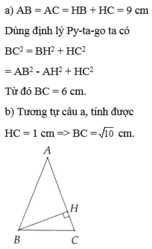
Ta thấy: AC=AB=HA+HC+1+8=9(cm) (do ABC là tam giác cân)
Áp dụng định lý Pytago vào tam giác vuông ABH tại H, ta có:
AH2+BH2=AB2
<=>12+BH2=92
<=>1+BH2=81
<=>BH2=80(1)
<=>BH=\(4\sqrt{5}\)(cm)
Xét tam giác HBC vuông tại B. Áp dụng định lý Pytago và kết quả (1) ta có:
BH2+HC2=BC2
<=>80+82=BC2
<=>BC2=80+64=144
<=>BC=12(cm)
Vậy BC=12cm