K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
US
1
12 tháng 11 2021
a) A1 = B3 (vì là cặp góc so le trong).
b) A2 = B2 (vì là cặp góc đồng vị).
c) B3 + A4 = 1800 (vì là hai góc trong cùng phía).
d) B4 = A2 (vì cùng bằng B2).
NA
3
R
3
18 tháng 8 2019
Bạn có thể lên vietjack, hoặc các trang mạng giải toán khác nhé!
TT
1
HP
14 tháng 9 2015
bài 36: 108 . 28 = (10 . 2)8 = 208
108 : 28 = (10 : 2)8 = 58
254 . 28 = (52)4 . 28 = 58 . 28 = (5 . 2)8 = 108
158 . 94 = 158 . (32)4 = 158 . 38 = (15 . 3)8 = 458
272 : 253 = (33)2 : (52)3 = 36 : 56 = \(\left(\frac{3}{5}\right)^6\)
bài 37: \(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{2^{10}}=\frac{\left(2^2\right)^5}{2^{10}}=\frac{2^{10}}{2^{10}}=1\)
\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2.3\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5.3^5}{\left(0,2\right)^6}=\frac{3^5}{0,2}=1215\)
\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}=\frac{2^7.3^6}{2^5.3^5.2^6}=\frac{2^7.3}{2^{11}}=\frac{3}{2^4}=\frac{3}{16}\)
\(\frac{6^3+3.6^2+3^3}{-13}=\frac{\left(2.3\right)^3+3.\left[\left(2.3\right)^2\right]+3^3}{-13}=\frac{2^3.3^3+3.2^2.3^2+3^3}{-13}=\frac{3^3.\left(2^3+2^2+1\right)}{-13}=\frac{3^3.13}{-13}\) = -33 = -27
HD
2
DT
26 tháng 2 2018
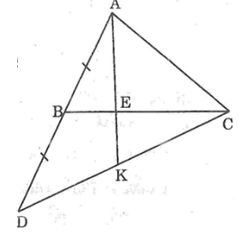
Trong ∆ACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/2 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ∆ACD.
Vì AK đi qua E nên AK là đường trung tuyến của ∆ACD
Suy ra K là trung điểm của CD
Vậy KD = KC.
26 tháng 2 2018
Không vẽ hình thì thôi :)
Xét tam giác ACD ta có:
CB là đường trung tuyến
Điểm E thuộc đoạn CB và \(CE=\frac{2}{3}CB\)
Suy ra E là trọng tâm của tam giác ACD
Nên AK là đường trung tuyến của tam giác ACD
Suy ra CK = KD
Vậy CK = KD ( đpcm )
Phải mò sách lớp 7 xem lại đấy :)
HD
1
26 tháng 2 2018
Trong ∆ACD ta có:
CB là đường trung tuyến kẻ từ đỉnh C
Mặt khác:
E ∈ BC và BE = 1/2 BC (gt)
Nên: CE = 2/3 CB
Suy ra: E là trọng tâm của ∆ACD.
Vì AK đi qua E nên AK là đường trung tuyến của ∆ACD
Suy ra K là trung điểm của CD
Vậy KD = KC.
15 tháng 6 2019
Link sách: Bài tập nâng cao và một số chuyên đề Toán 7 – Bùi Văn Tuyên - CHIA SẺ FULL
27 tháng 10 2019
mik ko chắc
a) Theo định nghĩa tập số hữu tỉ là tập hợp các số có thể viết dưới dạng phân số. Hay số hữu tỉ gồm các số thập phân hữu hạn và các số thập phân vô hạn tuần hoàn.
Số vô tỉ là tập hợp gồm các số thập phân vô hạn không tuần hoàn.
Do đó:
Q
∩
I
=
∅
b) Số thực là tập hợp gồm số hữu tỉ và số vô tỉ.
Do đó:
R
∩
I
=
I
ko chép đề