Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: Gọi giao điểm của AC và BD là O trong mp(ABCD)
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên (SAC) giao (SBD)=SO
Xét ΔSDC có
P,N lần lượt là trung điểm của DS,DC
=>PN là đường trung bình của ΔSDC
=>PN//SC
PN//SC
SC\(\subset\)(SBC)
PN không nằm trong mp(SBC)
Do đó: PN//(SBC)

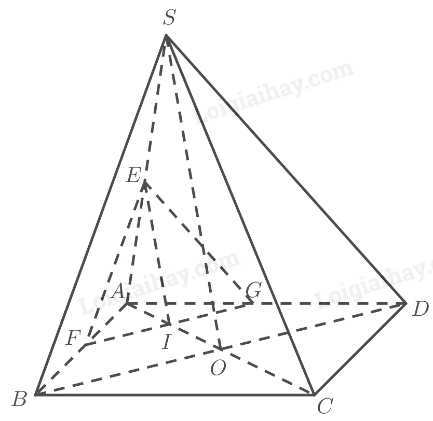
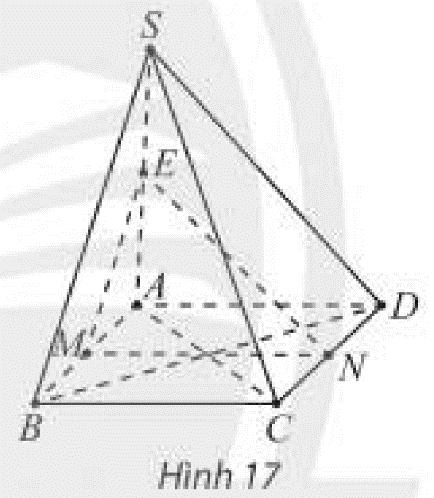
a) \(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(M\) là trung điểm của \(SA\)
\( \Rightarrow OM\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OM\parallel SC\\SC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow OM\parallel \left( {SBC} \right)\)
\(O\) là trung điểm của \(B{\rm{D}}\) (theo tính chất hình bình hành)
\(N\) là trung điểm của \(SD\)
\( \Rightarrow ON\) là đường trung bình của tam giác \(SB{\rm{D}}\)
\(\left. \begin{array}{l} \Rightarrow ON\parallel SB\\SB \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow ON\parallel \left( {SBC} \right)\)
\(\left. \begin{array}{l}OM\parallel \left( {SBC} \right)\\ON\parallel \left( {SBC} \right)\\OM,ON \subset \left( {OMN} \right)\end{array} \right\} \Rightarrow \left( {OMN} \right)\parallel \left( {SBC} \right)\)
b) \(O\) là trung điểm của \(AC\) (theo tính chất hình bình hành)
\(E\) là trung điểm của \(AB\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(ABC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow OE\parallel \left( {SBC} \right)\)
Do \(\left( {OMN} \right)\parallel \left( {SBC} \right)\) nên \(E \in \left( {OMN} \right)\)
Ta có:
\(\left. \begin{array}{l}EF \subset \left( {OMN} \right)\\\left( {OMN} \right)\parallel \left( {SBC} \right)\end{array} \right\} \Rightarrow EF\parallel \left( {SBC} \right)\)

1: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SAC) vuông góc (SBD)

A B C D N S M P H K
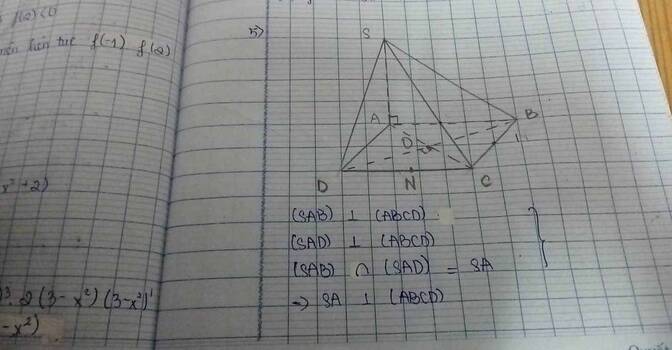
a) (SAB) và (SAD) cùng vuông góc (ABCD), (SAB) và (SAB) có giao tuyến SA => SA vuông góc (ABCD)
=> BC vuông góc SA. Mà BC vuông góc AB nên BC vuông góc (SAB).
Ta cũng có BD vuông góc AS, BD vuông góc AC vì ABCD là hình vuông
=> BD vuông góc (SAC) hay (SAC) vuông góc (SBD).
b) Gọi M là trung điểm của AB, CM cắt AD tại P, H thuộc CM sao cho AH vuông góc CM, K thuộc SH sao cho AK vuông góc SH.
Dễ thấy AN || CM => AN || (SCM) => d(AN,SC) = d(AN,SCM) = d(A,SCM) = d(A,SMP)
Ta có AH vuông góc MP, MP vuông góc AS => MP vuông góc (HAS) => (SMP) vuông góc (HAS)
Vì (SMP) và (HAS) có giao tuyến SH, AK vuông góc SH tại K nên d(A,SMP) = AK
Theo hệ thức lượng thì: \(\frac{1}{AK^2}=\frac{1}{AS^2}+\frac{1}{AM^2}+\frac{1}{AP^2}\)
\(\Rightarrow d\left(AN,SC\right)=d\left(A,SMP\right)=AK=\frac{AS.AM.AP}{\sqrt{AS^2AM^2+AM^2AP^2+AP^2AS^2}}\)
\(=\frac{a\sqrt{2}.\frac{a}{2}.a}{\sqrt{2a^2.\frac{a^2}{4}+\frac{a^2}{4}.a^2+a^2.2a^2}}=\frac{a\sqrt{22}}{11}.\)

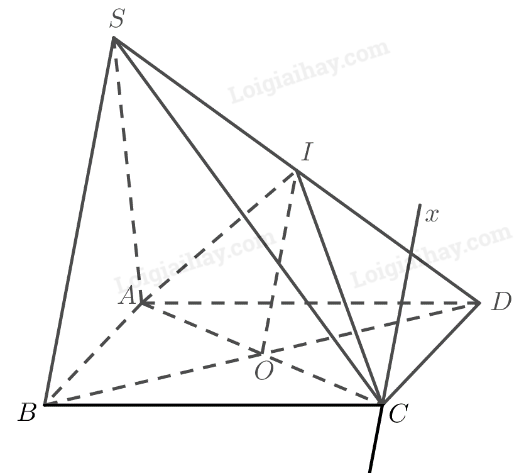
Gọi \(O\) là giao điểm của \(AC\) và \(BD\). Ta có:
\(I\) là trung điểm của \(SD\)
\(O\) là trung điểm của \(BD\) (theo tính chất hình bình hành)
\( \Rightarrow OI\) là đường trung bình của tam giác \(SB{\rm{D}}\)
\( \Rightarrow OI\parallel SB\)
Ta có:
\(\begin{array}{l}Cx = \left( {IAC} \right) \cap \left( {SBC} \right)\\SB = \left( {SB{\rm{D}}} \right) \cap \left( {SBC} \right)\\OI = \left( {IAC} \right) \cap \left( {SB{\rm{D}}} \right)\\SB\parallel OI\end{array}\)
Do đó theo định lí 2 về giao tuyến của ba mặt phẳng ta có: \(OI\parallel SB\parallel Cx\).

- Ta có: S là điểm chung của hai mặt phẳng (SAD) và (SBC)
Từ S kẻ Sx sao cho Sx // AD // BC. Vậy Sx là giao tuyến của hai mặt phẳng (SAD) và (SBC).
- Ta có: M, P là trung điểm của SA, SD. Suy ra MP // AD // BC
Có: N là điểm chung của hai mặt phẳng (MNP) và (ABCD)
Từ N kẻ NQ sao cho NQ // AD.
Vậy NQ là giao tuyến của hai mặt phẳng (MNP) và (ABCD).

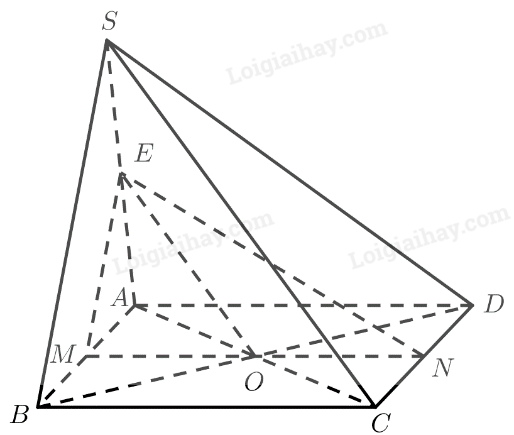
a) \(M\) là trung điểm của \(AB\)
\(N\) là trung điểm của \(C{\rm{D}}\)
\( \Rightarrow MN\) là đường trung bình của hình bình hành \(ABCD\)
\( \Rightarrow MN\parallel A{\rm{D}}\parallel BC\)
Ta có:
\(\begin{array}{l}\left. \begin{array}{l}MN\parallel BC\\BC \subset \left( {SBC} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SBC} \right)\\\left. \begin{array}{l}MN\parallel A{\rm{D}}\\A{\rm{D}} \subset \left( {SA{\rm{D}}} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {SA{\rm{D}}} \right)\end{array}\)
b) \(M\) là trung điểm của \(AB\)
\(E\) là trung điểm của \(SA\)
\( \Rightarrow ME\) là đường trung bình của tam giác \(SAB\)
\(\left. \begin{array}{l} \Rightarrow ME\parallel SB\\ME \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SB\parallel \left( {MNE} \right)\)
Gọi \(O\) là giao điểm của \(AC\) và \(BD\)
\( \Rightarrow O\) là trung điểm của \(AC\) và \(O,M,N\) thẳng hàng
Mà \(E\) là trung điểm của \(SA\)
\( \Rightarrow OE\) là đường trung bình của tam giác \(SAC\)
\(\left. \begin{array}{l} \Rightarrow OE\parallel SC\\OE \subset \left( {MNE} \right)\end{array} \right\} \Rightarrow SC\parallel \left( {MNE} \right)\)

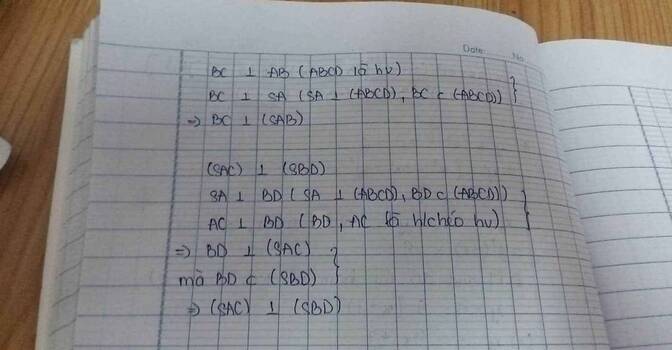
a, Xét (ABCD) có AC giao BD = O
Xét (SAC);(SBD) có
S là điểm chung t1; O là điểm chung t2
=> SO là giao tuyến 2 mp trên
b, Xét tam giác SDC có PN là đường tb tam giác
=> NP // SC ; SC \(\subset\)(SBC)
=> NP // (SBC)
b, Xét (ABCD) kẻ MN cắt AD tại K
Do K thuộc AD => K \(\subset\)(SAD)
=> PK giao SA tại Q
Xét tam giác MNC và tam giác KND có
^NMC = ^KND (sole) ; NC = ND (N là trung điểm); ^MNC = ^KND = ^KND (đối đỉnh)
=> tam giác MNC = tam giác KND (g.c.g)
=> DK = MC (2 cạnh tương ứng)
=> \(\dfrac{AK}{AD}=\dfrac{AD+DK}{AD}=\dfrac{AD+MC}{AD}=\dfrac{AD+\dfrac{BC}{2}}{AD}=\dfrac{AD+\dfrac{AD}{2}}{AD}=\dfrac{3}{2}\)
Do AD = BC ( ABCD là hbh)
Xét tam giác DSC có \(\dfrac{DP}{SP}=\dfrac{DN}{NC}=1\)theo Ta lét, N là trung điểm DC
Theo Menelaus ta có
\(\dfrac{SQ}{SA}.\dfrac{AI}{AD}.\dfrac{DP}{SP}=1\Leftrightarrow\dfrac{SQ}{SA}.\dfrac{3}{2}=1\Leftrightarrow\dfrac{SQ}{SA}=\dfrac{2}{3}\)
a) Gọi �O là giao điểm của ��AC và ��BD.
Xét hai mp (���)(SAC) và (���)(SBD) có
�S là điểm chung của hai mặt phẳng.
�∈��⊂(���)O∈AC⊂(SAC)
�∈��⊂(���)O∈BD⊂(SBD)
Suy ra �O là điểm chung của hai mặt phẳng.
Vậy giao tuyến của hai mặt phẳng (���)(SAC) và (���)(SBD) là ��SO.
NP
⊂(SBC)NP // SCSC⊂(SBC)
⇒��⇒NP // (���).(SBC).
⎧NP⊂(SBC)NP // SCSC⊂(SBC)
⇒��⇒NP // (���).(SBC).
b) Gọi E là giao AC và MN
Có: NP//SC;EQ là giao tuyển của (PMN) và (SAC)
⇒IQ // ��⇒����=����SC=> \(\dfrac{CI}{CA}\)=\(\dfrac{SQ}{SA}\)
Mà CI=\(\dfrac{1}{4}CA\)
=>\(\dfrac{SQ}{SA}=\dfrac{CI}{CA}=\dfrac{1}{4}\)