Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi phương trình đường thẳng \(d:ax + by + c = 0\)
a) Từ hình a) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B( - 5;0)\)
\( \Rightarrow \left\{ \begin{array}{l}b.2 + c = 0\\ - 5a + c = 0\end{array} \right. \Rightarrow c = 5a = - 2b\)
Chọn \(a = 2 \Rightarrow b = - 5;c = 10\) và \(d:2x - 5y + 10 = 0\)
Điểm O (0;0) thuộc miền nghiệm và \(2.0 - 5.0 + 10 = 10 > 0\)
Vậy bất phương trình cần tìm là \(2x - 5y + 10 > 0\)
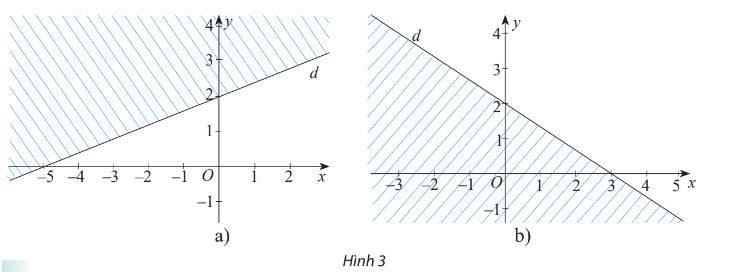
b) Từ hình b) ta thấy d đi qua hai điểm\(A(0;2)\) và \(B(3;0)\)
\( \Rightarrow \left\{ \begin{array}{l}2b + c = 0\\3a + c = 0\end{array} \right. \Rightarrow - c = 3a = 2b\)
Chọn \(a = 2 \Rightarrow b = 3;c = - 6\) và \(d:2x + 3y - 6 = 0\)
Điểm O (0;0) không thuộc miền nghiệm và \(2.0 + 3.0 - 6 = - 6 < 0\)
Vậy bất phương trình cần tìm là \(2x + 3y - 6 > 0\)

Tham khảo:
Để pha x lít nước cam loại I cần 30x g bột cam,
Để pha y lít nước cam loại II cần 20y g bột cam,
Vì Cúc chỉ có thể dùng không quá 100 gam bột cam nên ta có bất phương trình \(30x + 20y \le 100\)
\( \Leftrightarrow 3x + 2y - 10 \le 0\)
Vẽ đường thẳng \(\Delta :3x + 2y - 10 = 0\) đi qua hai điểm \(A(0;5)\) và \(B\left( {2;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(3.0 + 2.0 - 10 = - 10 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
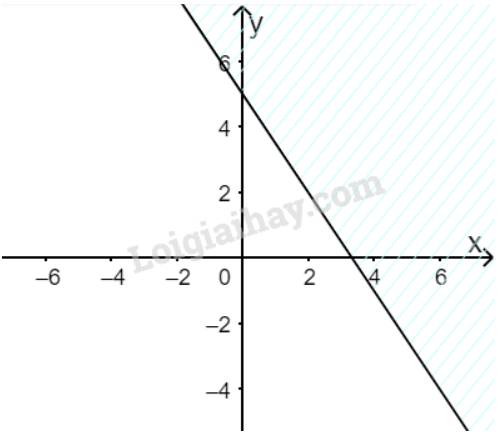

Gọi x là số kg cam
y là số kg quýt
Theo đề , ta có
\(\hept{\begin{cases}x+y=6\\15000x+20000y=100000\end{cases}}\)
\(\hept{\begin{cases}x=4\\y=2\end{cases}}\)

+) Số cách chọn 5 bông hoa bất kì trong 110 bông hoa là: \(C_{110}^5\) ( cách chọn)
+) Số cách chọn 5 bông cúc trong 60 bông cúc là: \(C_{60}^5\) ( cách chọn)
+) Số cách chọn 5 bông hoa hồng trong 50 bông hồng là: \(C_{50}^5\) ( cách chọn)
+) Số cách chọn 5 bông hoa gồm cả 2 loại trong 110 bông hoa là: \(C_{110}^5 - C_{60}^5 - C_{50}^5\) ( cách chọn)

Gọi x và y lần lượt là giá tiền mỗi quả quýt và mỗi quả cam. (x > 0; y > 0)
Vân mua 10 quả quýt, 7 quả cam hết 17800 đồng nên ta có:
10x + 7y = 17800
Lan mua 12 quả quýt, 6 quả cam hết 18000 đồng nên ta có:
12x + 6y = 18000
Từ đó ta có hệ:
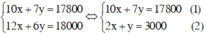
Từ (2) rút ra được y = 3000 – 2x, thay vào (1) ta được :
10x + 7.(3000 – 2x) = 17800
⇔ 10x + 21000 – 14x = 17800
⇔ 4x = 3200 ⇔ x = 800 (thỏa mãn)
Thay x = 800 vào y = 3000 – 2x ta được y = 1400 (thỏa mãn)
Vậy giá tiền một quả quýt là 800đ và giá tiền một quả cam là 1400đ.
Dì Ly mang 100000 đồng đi mua cam. Dì mua 8 quả cam, trung bình mỗi quả nặng 0,25 kg. Biết mỗi kg cam là 35000 đồng. Tính số tiền dì Ly còn lại sau khi mua cam\(\left[{}\begin{matrix}&&&&\\&&&&\end{matrix}\right.\begin{matrix}\\\\\\\end{matrix}\right.\)


2 quả cam ứng với số phần là:
\(\frac{1}{5}\)-\(\frac{1}{6}\)=\(\frac{1}{30}\)(phần)
vậy số cam cúc đem đi bán là :
2:\(\frac{1}{30}\)=60(quả)