Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 1:
a) Xét ΔOAB và ΔODC có
\(\widehat{OAB}=\widehat{ODC}\)(hai góc so le trong, AB//DC)
\(\widehat{AOB}=\widehat{DOC}\)(hai góc đối đỉnh)
Do đó: ΔOAB∼ΔODC(g-g)
⇒\(\frac{OA}{OD}=\frac{OB}{OC}\)
hay \(OA\cdot OC=OB\cdot OD\)(đpcm)
b) Xét ΔAHO và ΔDKO có
\(\widehat{AHO}=\widehat{DKO}\left(=90^0\right)\)
\(\widehat{AOH}=\widehat{DOK}\)(hai góc đối đỉnh)
Do đó: ΔAHO∼ΔDKO(g-g)
⇒\(\frac{OH}{OK}=\frac{AO}{DO}\)(các cặp cạnh tương ứng)
mà \(\frac{AO}{DO}=\frac{AB}{CD}\)(ΔOAB∼ΔODC)
nên \(\frac{OH}{OK}=\frac{AB}{CD}\)(đpcm)
Bài 2:

Bài 3:
a) Xét ΔAHB và ΔBCD có
\(\widehat{AHB}=\widehat{BCD}\left(=90^0\right)\)
\(\widehat{ABH}=\widehat{BDC}\)(hai góc so le trong, AB//DC)
Do đó: ΔAHB∼ΔBCD(g-g)
b) Xét ΔADH và ΔBDA có
\(\widehat{ADH}\) chung
\(\widehat{AHD}=\widehat{BAD}\left(=90^0\right)\)
Do đó: ΔADH∼ΔBDA(g-g)
⇒\(\frac{AD}{BD}=\frac{DH}{DA}\)
hay \(AD^2=BD\cdot DH\)(đpcm)
c) Áp dụng định lí pytago vào ΔADB vuông tại A, ta được:
\(BD^2=AD^2+AB^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
\(\Leftrightarrow BD=\sqrt{100}=10cm\)
Ta có: \(AD^2=BD\cdot DH\)(cmt)
⇔\(6^2=10\cdot DH\)
hay \(DH=\frac{6^2}{10}=3,6cm\)
Áp dụng định lí pytago vào ΔAHD vuông tại H, ta được:
\(AD^2=AH^2+DH^2\)
\(\Leftrightarrow AH^2=AD^2-DH^2=6^2-3.6^2=23,04\)
hay \(AH=\sqrt{23,04}=4,8cm\)
Vậy: DH=3,6cm; AH=4,8cm

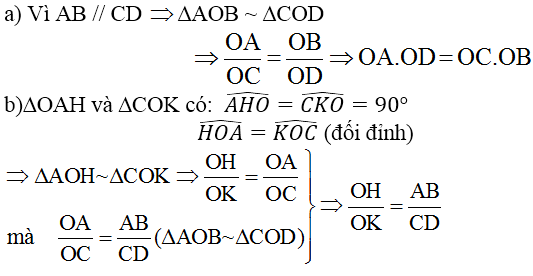
a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)