Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn trục tọa độ thẳng đưgs, chiều dương hướng xuống.
Gốc tọa độ tại vị trí thả viên bi A.
Gốc thời gian là lúc viên bi A rơi.
Ptrình chuyển động:
+ Viên bi A: \(y_1=y_{02}+\dfrac{1}{2}gt^2=\dfrac{1}{2}gt^2\)
+ Viên bi B: \(y_2=y_{02}+\dfrac{1}{2}g\left(t-t_0\right)=10+\dfrac{1}{2}g\left(t-1\right)^2\)
Khi 2 viên bi gặp nhau thì: \(y_1=y_2\)
\(\Leftrightarrow\dfrac{1}{2}gt^2=10+\dfrac{1}{2}g\left(t-1\right)^2\)
\(\Leftrightarrow t=1,5s\)
Vậy.............

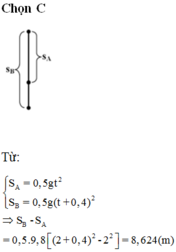
Chọn thời điểm viên bi A bắt đầu rơi làm mốc thời gian. Nếu gọi t là thời gian rơi của viên bi A thì thời gian rơi của viên bi B sẽ là t' = t + 0,5. Như vậy quãng đường mà viên bi A và B đã đi được tính theo các công thức :
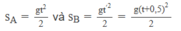
Từ đó suy ra khoảng cách giữa hai viên bi sau khoảng thời gian 2 s kể từ khi bi A bắt đầu rơi
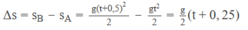
Suy ra ∆ s ≈ 11m

Gọi vận tốc đầu của hai viên bi là O
Ta có sau khi viên bi 1 đi được 1s thì viên bi 2 đi được 1,5 giây
ta có \(\Delta S=S2-S1=\dfrac{1}{2}g.\left(1,5\right)^2-\dfrac{1}{2}.g.\left(1\right)^2=6,25m\)
( đáng lẽ pt là vot+0,5gt2 nhưng vo = o rồi nhé ) ten lấy g= 10 m/s2 hay là bạn lấy g= 9,8 m/s2 cũng được nhé!

Giải :
Chọn trục toạ độ thẳng đứng, chiều dương hướng xuống gốc toạ độ tại vị trí bạn Giang thả ở tầng 19, gốc thời gian lúc bi A rơi.
Phương trình chuyển động của viên bi A: với x 01 = 0 m ; v 01 = 0 m / s ⇒ x 1 = 1 2 g t 2
Phương trình chuyển động của viên bi B: với x 02 = 10 m ; v 02 = 0 m / s thả rơi sau 1s so vói gốc thời gian x 2 = 10 + 1 2 g ( t − 1 ) 2
Khi 2 viên bi gặp nhau: x 1 = x 2 ⇔ 1 2 g t 2 = 10 + 1 2 g ( t − 1 ) 2 ⇒ t = 1 , 5 s và cách vị trí thả của giang là x 1 = 1 2 g . t 2 = 1 2 .10.1 , 5 2 = 112 , 5 m

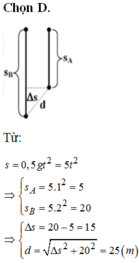
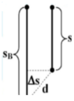
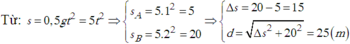
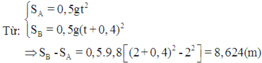
B