Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A = \(\dfrac{9}{1.2}\)+ \(\dfrac{9}{2.3}\)+\(\dfrac{9}{3.4}\)+......+\(\dfrac{99}{99.100}\)
A = 9( \(\dfrac{1}{1.2}\)+\(\dfrac{1}{2.3}\)+\(\dfrac{1}{3.4}\)+.......+\(\dfrac{1}{99.100}\))
A = 9( 1-\(\dfrac{1}{2}\)+\(\dfrac{1}{2}\)-\(\dfrac{1}{3}\)+........+\(\dfrac{1}{99}\)-\(\dfrac{1}{100}\))
A = 9 ( 1 - \(\dfrac{1}{100}\))
A = 9 . \(\dfrac{99}{100}\)
A = \(\dfrac{891}{100}\)
\(A=\dfrac{9}{1\cdot2}+\dfrac{9}{2\cdot3}+\dfrac{9}{3\cdot4}+...+\dfrac{9}{98\cdot99}+\dfrac{9}{99\cdot100}\)
\(=9\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+\dfrac{1}{3\cdot4}+...+\dfrac{1}{98\cdot99}+\dfrac{1}{99\cdot100}\right)\)
\(=9\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=9\left(1-\dfrac{1}{100}\right)\)
\(=9\left(\dfrac{100}{100}-\dfrac{1}{100}\right)\)
\(=9\cdot\dfrac{99}{100}\)
\(=\dfrac{891}{100}\)

1)Tính
a)\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+..........+\dfrac{1}{9.10}\)
=\(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+.....+\dfrac{1}{9}-\dfrac{1}{10}\)
\(=1-\dfrac{1}{10}\)
\(=\dfrac{9}{10}\)
b)\(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+.........+\dfrac{1}{99.100}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+..............+\dfrac{1}{99}-\dfrac{1}{100}\)
\(=1-\dfrac{1}{100}\)
\(=\dfrac{99}{100}\)
2) tìm x
\(a\)) \(\dfrac{2}{5}+\dfrac{4}{5}x-\dfrac{7}{5}\)\(=\dfrac{9}{5}\)
\(\dfrac{4}{5}x+\dfrac{7}{5}=\dfrac{9}{5}-\dfrac{2}{5}\)
\(\dfrac{4}{5}x+\dfrac{7}{5}=\dfrac{7}{5}\)
\(\dfrac{4}{5}x=\dfrac{7}{5}-\dfrac{7}{5}\)
\(\dfrac{4}{5}x=0\)
\(x=0:\dfrac{4}{5}\)
\(x=0\)
b)\(\dfrac{2}{5}x-\dfrac{6}{4}=\dfrac{8}{5}\)
\(\dfrac{2}{5}x=\dfrac{8}{5}+\dfrac{6}{4}\)
\(\dfrac{2}{5}x=\dfrac{31}{10}\)
\(x=\dfrac{31}{10}:\dfrac{2}{5}\)
\(x=\dfrac{31}{4}\)
1. Tính:
a. \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+...+\dfrac{1}{9.10}\)
= \(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{9}-\dfrac{1}{10}\)
= \(\dfrac{1}{1}-\dfrac{1}{10}\)
= \(\dfrac{10}{10}-\dfrac{1}{10}\)
= \(\dfrac{9}{10}\)
b. \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
= \(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
= \(\dfrac{1}{1}-\dfrac{1}{100}\)
= \(\dfrac{100}{100}-\dfrac{1}{100}\)
= \(\dfrac{99}{100}\)
2. Tìm x, biết:
a. \(\dfrac{2}{5}+\dfrac{4}{5}x-\dfrac{7}{5}=\dfrac{9}{5}\)
\(\dfrac{4}{5}x-\dfrac{7}{5}=\dfrac{9}{5}-\dfrac{2}{5}\)
\(\dfrac{4}{5}x-\dfrac{7}{5}=\dfrac{7}{5}\)
\(\dfrac{4}{5}x=\dfrac{7}{5}+\dfrac{7}{5}\)
\(\dfrac{4}{5}x=\dfrac{14}{5}\)
\(x=\dfrac{14}{5}:\dfrac{4}{5}\)
\(x=\dfrac{14}{5}.\dfrac{5}{4}\)
\(x=14.\dfrac{1}{4}\)
\(x=\dfrac{14}{4}\)
Vậy \(x=\dfrac{14}{4}\)
b. \(\dfrac{2}{5}x-\dfrac{6}{4}=\dfrac{8}{5}\)
\(\dfrac{2}{5}x=\dfrac{8}{5}+\dfrac{6}{4}\)
\(\dfrac{2}{5}x=\dfrac{32}{20}+\dfrac{30}{20}\)
\(\dfrac{2}{5}x=\dfrac{62}{20}\)
\(\dfrac{2}{5}x=\dfrac{31}{10}\)
\(x=\dfrac{31}{10}:\dfrac{2}{5}\)
\(x=\dfrac{31}{10}.\dfrac{5}{2}\)
\(x=\dfrac{31}{2}.\dfrac{2}{2}\)
\(x=\dfrac{31}{2}.1\)
\(x=\dfrac{31}{2}\)
Vậy \(x=\dfrac{31}{2}\)
bài này mk tự làm ko sao chép trên mạng![]()
nếu thấy đúng thì tick đúng cho mk nha![]()

\(A=\dfrac{9}{1.2}+\dfrac{9}{2.3}+\dfrac{9}{3.4}+...+\dfrac{9}{98.99}+\dfrac{9}{99.100}\)
\(=9\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\right)\)
\(=9\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=9\left(1-\dfrac{1}{100}\right)\)
\(=9.\dfrac{99}{100}\)
\(=\dfrac{891}{100}\)
\(A=\dfrac{9}{1.2}+\dfrac{9}{2.3}+\dfrac{9}{3.4}+...+\dfrac{9}{98.99}+\dfrac{9}{99.100}\)
\(=9.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\right)\)
\(=9.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(=9.\left(1-\dfrac{1}{100}\right)\)
\(=9.\dfrac{99}{100}\)
\(=\dfrac{891}{100}\).

Bài 10:
a: Để A là phân số thì n+2<>0
hay n<>-2
b: Khi n=0 thì A=3/2
Khi n=2 thì A=3/(2+2)=3/4
Khi n=-7 thì A=3/(-7+2)=-3/5
Bài 9:
1)9/x = -35/105 2) 12/5 = 32/x 3)x/2 = 32/x x = 9. (-35)/105 x.12/5 = x.32/x 2x.x/2 = 2x.32/x
x = -3 x.12/5=32 xx = 2.32
x= 32:12/5 x^2 = 2.32
x = 40/3 x^2 = 64
x = 8
4) x-2/4 = x-1/5
5(x-2) = 4(x-1)
5x - 10 = 4x - 4
5x - 4x = 10 - 4
x = 6
Bài 10:Cho biểu thức A=3/n+2
a) Để A là phân số thì mẫu số phải khác 0
Do đó: n + 2 ≉ 0. Suy ra: n ≉ -2
b) Khi n = 0 thì A = 3/0+2 = 3/2
Khi n = 2 thì A = 3/2+2 = 3/4
Khi n = -7 thì A = 3/-7+2 = 3/-5

Gợi ý: Sử dụng tính chất phân phối của phép nhân đối với phép cộng để nhóm thừa số chung ra ngoài.

\(C=\dfrac{6}{7}+\dfrac{5}{8}:5-\dfrac{3}{16}.\left(-2^2\right)\\ C=\dfrac{6}{7}+\dfrac{5}{8}.\dfrac{1}{5}-\dfrac{3}{16}.\left(-4\right)\\ C=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{16}.\left(-4\right)\\ C=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{16}.\dfrac{-4}{1}\\ C=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{-3}{4}\\ C=\dfrac{48}{56}+\dfrac{7}{56}-\dfrac{-42}{56}\\ C=\dfrac{97}{56}\)

a) \(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+....+\dfrac{1}{99.100}\)
= \(\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+....+\dfrac{1}{99}-\dfrac{1}{100}\)
=\(\dfrac{1}{1}+0+0+...+0-\dfrac{1}{100}\)
=\(1-\dfrac{1}{100}\)
= \(\dfrac{99}{100}\)
a) 11.2+12.3+13.4+....+199.10011.2+12.3+13.4+....+199.100
= 11−12+12−13+13−14+....+199−110011−12+12−13+13−14+....+199−1100
=11+0+0+...+0−110011+0+0+...+0−1100
=1−11001−1100
= 99100
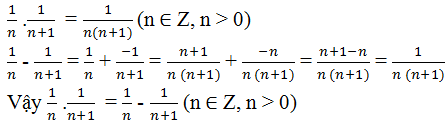

bài 2:
\(A=9.\left(\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{98.99}+\dfrac{1}{99.100}\right)\)
\(A=9.\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{98}-\dfrac{1}{99}+\dfrac{1}{99}-\dfrac{1}{100}\right)\)
\(A=9.\left(1-\dfrac{1}{100}\right)=9.\left(\dfrac{100}{100}-\dfrac{1}{100}\right)=\dfrac{891}{100}\)
bài 3:
\(=>\dfrac{x}{3}=\dfrac{5}{8}+\dfrac{1}{8}=\dfrac{8}{8}=1=\dfrac{3}{3}\)
\(=>x=3\)